In Geometry, a pentagon is a two-dimensional figure having 5 sides and 5 angles. In a pentagon, an angle is formed when the two sides of the pentagon share a common point. Since the number of vertices in a pentagon is five, the number of angles in a pentagon is five. In this article, we are going to discuss the angles in a pentagon, such as interior angles, exterior angles, the sum of angles in a pentagon, etc., in detail with many examples.

Before discussing the angles in a pentagon, let us first discuss what a pentagon is? and different types of pentagons.

Pentagon and its Types

A pentagon is a closed two-dimensional polygon with 5 sides and 5 angles. Based on the properties, a pentagon can be classified into different types. They are:

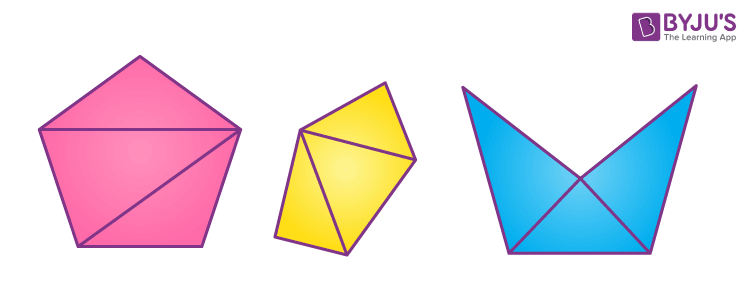
Regular Pentagon: A pentagon having all its sides and interior angles are equal.

Irregular Pentagon: All the sides of a pentagon are not equal and the interior angles are not of the same measurement.

Convex Pentagon: All the interior angles are less than 180° and all the vertices point outwards. A regular pentagon is a convex pentagon.

Concave Pentagon: If one of the interior angles of a pentagon is greater than 180° and if one of the vertices points inward, then it is called a concave polygon.

The following figure depicts the definition of a regular pentagon, irregular pentagon, and concave pentagon respectively.

 

Sum of Angles in a Pentagon

The sum of angles in a pentagon is the sum of five angles of the pentagon. Now let us discuss the sum of interior and exterior angles of a pentagon.

Sum of Interior Angles in a Pentagon

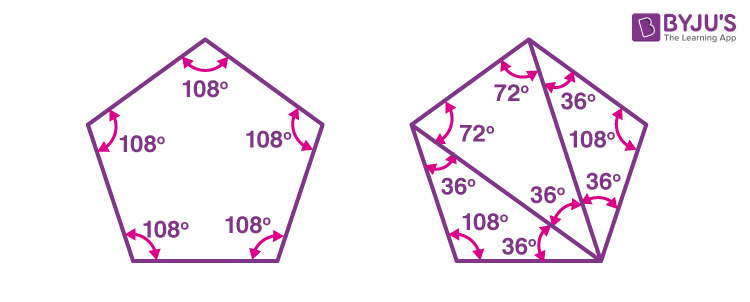
Pentagon is formed from three triangles, so the sum of angles in a pentagon = 3 × 180° = 540°.

We can also calculate the sum of interior angles of the pentagon in the following way:

We know that the sum of the interior angles of a polygon of n sides = (n – 2) × 180°.

Since a pentagon has 5 sides, the sum of interior angles of a pentagon is = (5-2)× 180° [where n=5]

= 3× 180°= 540°.

Hence, the sum of interior angles of a pentagon is 540°.

Sum of Exterior Angles in a Pentagon

We know that the formula to calculate the sum of interior angles of a polygon is (n – 2) × 180°.

Hence, each interior angle = [(n – 2) × 180°]/n.

We know that each exterior angle is supplementary to the interior angle.

Thus, from the above formula, we can derive each exterior angle = [180°n -180°n + 360°]/n = 360°/n

Therefore, the sum of exterior angles of a polygon = n(360°/n).

As, the number of sides in a pentagon is 5, n=5.

Thus, the sum of exterior angles of a pentagon = 5(360°/5) = 360°.

Interior Angle of a Regular Pentagon

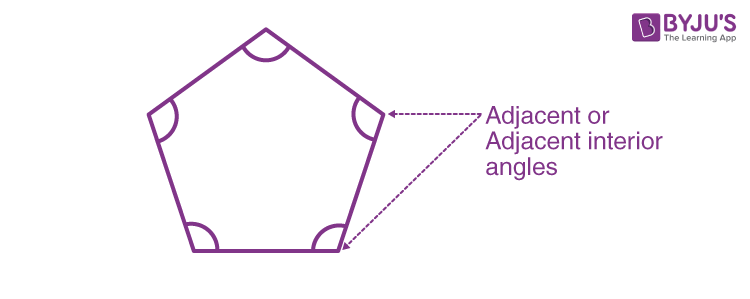
The angles formed by two adjacent pairs of sides are called interior angles of a pentagon.

Number of sides = Number of vertices = Number of interior angles = 5

Two interior angles that share a common side are called adjacent angles or adjacent interior angles.

A regular pentagon has all its five sides equal and all five angles are also equal. Hence, the measure of each interior angle of a regular pentagon is given by the below formula.

Measure of each interior angle = [(n – 2) × 180°]/n = 540°/5 = 108°.

Here, n = Number of sides

Read more:-

• Types Of Polygon
• Area Of Polygon
• Perimeter Of Polygons
• Congruence Of Triangles Class 9

Exterior Angle of a Regular Pentagon

Exterior angles of a pentagon are the angles formed outside the pentagon with its sides when the sides of the pentagon are extended. Each exterior angle of a pentagon is equal to 72°.

Since the sum of exterior angles of a regular pentagon is equal to 360°, the formula to calculate each exterior angle of a regular pentagon is given as follows:

The measure of each exterior angle of a pentagon = 360°/n = 360°/5 = 72°.

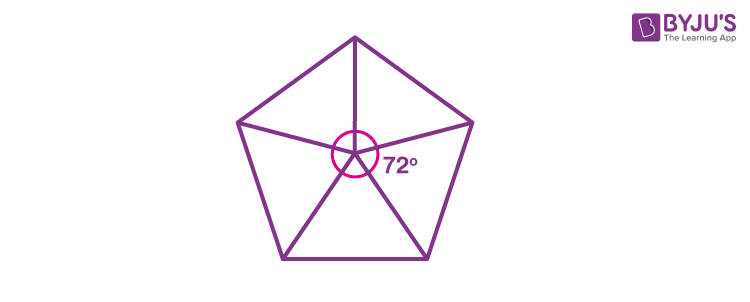
Central Angle of a Pentagon

The measure of the central angle of a regular pentagon makes a circle, i.e. total measure is 360°. If we divide pentagon into five congruent triangles, then the angle at one vertex of them will be 72° (360°/5 = 72°).

Angles in a Pentagon Examples

Example 1:

Three angles of a pentagon are 80°, 70° and 100°, then the other two angles can be 145° and 145° or 120° and 180°?

Solution:

Given three angles are 80°, 70° and 100°.

Sum of three angles = 80° + 70° + 100° = 250°

We know that the sum of all the five angles of a pentagon is 540°.

Sum of the other two angles = 540° – 250° = 290°

Now,

145° + 145° = 290°

120° + 180° = 300°

Hence, the other two angles of a pentagon are 145° and 145°.

Example 2:

Find the value of x from the below-given figure of the pentagon.

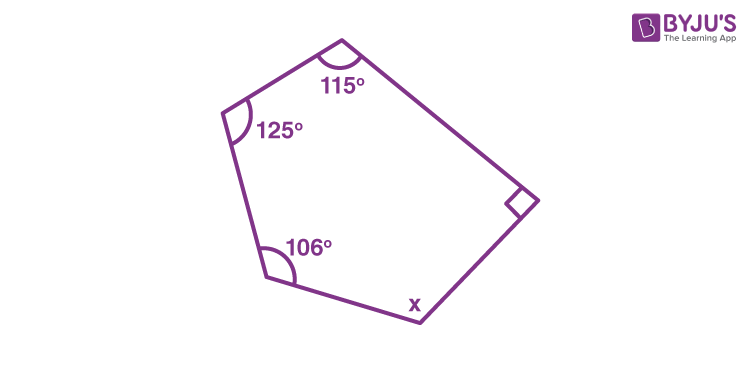
Solution:

Given that, one of the angles of a pentagon is a right angle, i.e. 90°.

By angle sum property of a pentagon,

x + 90° + 115° + 125° + 106° = 540°

x + 436° = 540°

x = 540° – 436°

x = 104°

Stay tuned with BYJU’S – The Learning App and download the app to learn all Maths-related concepts easily by exploring more videos.