An equation in the form of ax+by+c, where a,b and c are real numbers and a,b are not equal to zero, is called a linear equation in two variables. Whereas in pair of linear equation in two variables, we deal with two such equations.  The solution of such equations is a point on the line representing the equation. This topic is widely explained in Class 10 Maths Chapter 3.

An equation is an expression with equality sign on both sides. A polynomial involves a mathematical expression with powers of the variables as non-negative integers. For example, x⁴ + 3x³ + 2x⁹ is a polynomial but x^3/5+ 3x^0.6 is not a polynomial. While defining polynomials we should know about the concept of ‘degree’. A degree can be defined as the highest power of the variable in the given polynomial. A polynomial with degree 1 is called a linear polynomial. A polynomial with degree 2 is called a quadratic polynomial and a polynomial with degree 3 is called a cubic polynomial.

In this article, where we are learning about linear equations, the polynomial here is of degree 1.

Pair Of Linear Equation In Two Variables Notes

In earlier classes, we have studied about linear equation in one variable, and we know how to solve it. If there were one variable and one equation, we used to solve it easily, but in this case, we have two variables and two equations. One thing is for certain that we need two different sets of linear equations in order to find out the two different unknowns. If one equation is given and two variables are asked to be solved, we will not get the particular solution.

For example,

3x + 2y = 9 and 5x + y = 10

These simultaneous equations can be solved, and we can arrive at a particular solution from these but on the other hand,

6x + 7y = 9

Here, we cannot get a particular solution for this as there is only one condition given, and we have two unknowns. We can rewrite the above equation as:

y = (9-6x)/7

Depending on the values of x, the values of y will change accordingly. So, one unique solution is not possible.

Thus, it can be clearly said that in order to get a particular solution of systems, of linear equations in two variables, we need two different sets of independent conditions.

Representation of Pair Of Linear Equation In Two Variables

The pair of linear equations can be solved and represented by two methods:

1. Graphical Method
2. Algebraic Method

The general representation of a pair of linear equation in two variables say x and y is given by:

a₁x + b₁y + c₁ = 0  ……………(1)

a₂x + b₂y + c₂ = 0 ……………(2)

where a₁, b₁, c₁, a₂, b₂, c₂ are all real numbers and a₁² + b₁² ≠ 0, a₂²+ b₂² ≠ 0.

If the pair of linear equations are given in the form of a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = 0, then three conditions arises here:

1. If the pair of linear equations is consistent, then: a₁/a₂ ≠ b₁/b₂
2. If the pair of linear equations is inconsistent, then: a₁/a₂ = b₁/b₂ ≠ c₁/c₂
3. If the pair of linear equations is dependent and consistent, then: a₁/a₂ = b₁/b₂ = c₁/c₂

For example, 2x-y = -1 and 3x + 2y = 9 are pair of linear equations with variables x and y. In the below diagram you can see we have found the solutions for both equations by putting the value of x to get the value of y.

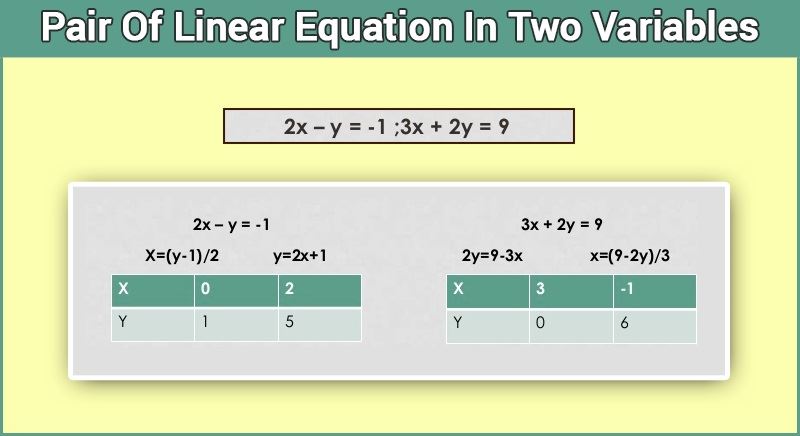
In the same way, we can find solutions for the following examples:

• 2x+3y-4 = 0 and 3x+2y+4 = 0
• 6x=y and 4x-3y-5 = 0

But what if we have to represent these equations in the graph. Let us learn in the next section.

Graphical Representation

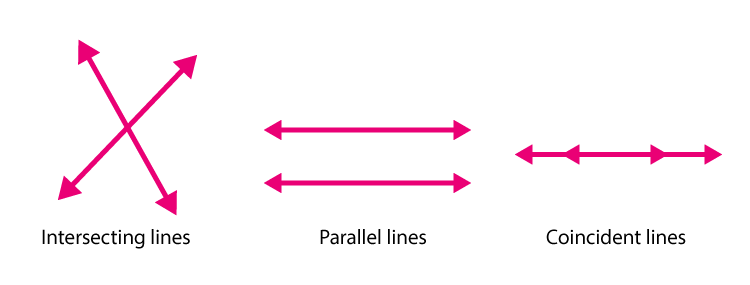
You have learned in Class 9, if there are two lines present in a plane, then there could be three possibilities, such as;

• The two lines intersect with each other
• Or they are parallel to each other
• Or they coincide each other

The above three conditions can be represented graphically as shown below:

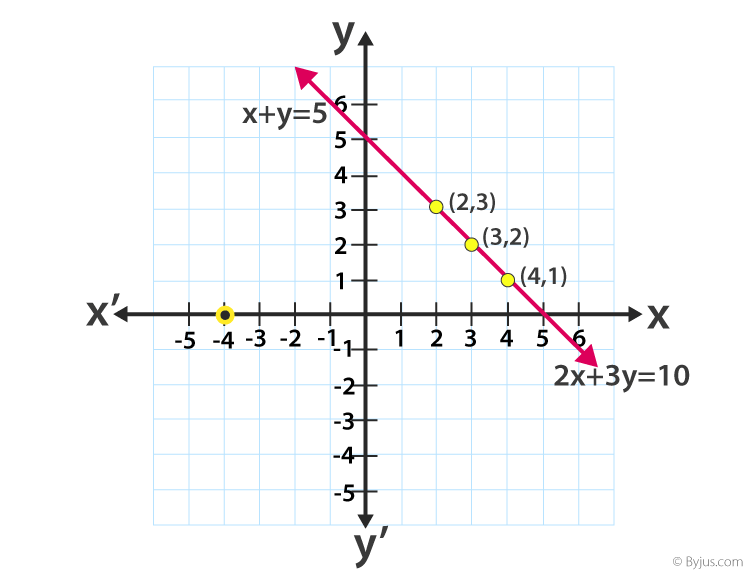
Now let us consider a pair of linear equations, x + y = 5, 2x + 2y = 10. To represent these two linear equations in a graph with a straight line, first, we need to find the solutions. After finding the solutions we get the distinct values of x and y. Hence, it can be represented as:

Algebraic Methods of Solving a Pair of Linear Equations

Let us start with the practical application of simultaneous linear equations in our day-to-day lives. Pair of linear equations can find its way in every possible scenario. Say you went to the fish market to buy fishes. There were two sizes of fishes available. The fisherman told that the total price of the smaller fish is 3 times the total price of the bigger fish. Also, the total money that you bought from your home is Rs.100. Can you find out how much did you spent to buy the two types of fishes?

Let us understand this mathematically,

Let the price of the smaller fish be Rs.x and the price of the bigger fish be Rs.y.

As per the first condition, x = 3y…………(1)

And as per the second condition, x + y = 100……………(2)

In order to find the solution, we need to solve both the equations and find the value of both x and y. The coordinates (x, y) can be placed easily in a graph. But the graphical method is not convenient in cases when the point representing the solution of the linear equations has non-integral coordinates like (√3, 2 √7) , (–1.75, 3.3), (4/13, 1/18), etc. Hence, we use algebraic methods to solve such cases.

There are following types of algebraic methods to solve a pair of linear equations:

1. Substitution Method
2. Elimination Method
3. Cross-Multiplication Method

More explanation about how to solve these equations and different methods to solve please visit our website www.byjus.com or download BYJU’s-the learning app.