Pentagonal Prism
What is a Pentagonal Prism?
A pentagonal prism is a prism that has two pentagonal bases like top and bottom and five rectangular sides. It is a type of heptahedron with 7 faces, 10 vertices and 15 edges. A pentagonal prism can have pentagonal bases which give five sides. A pentagonal prism is also known as five-sided polygon prism.
To recall, the prism shape, in maths, is a three-dimensional box i.e. a solid figure with a uniform cross-section and has two common bases.
- Face: A flat side of a 3-dimensional object
- Base: One of the two parallel and congruent sides of an object
- Edge: Intersection of two faces on a solid object. This is a line.
- Vertex: Joining point of two edge sides.
Types of Pentagonal Prisms
There are two types of pentagonal prisms which are:
- Regular Pentagonal Prisms
- Right Pentagonal Prisms
Regular Pentagonal Prism
If all the sides of the pentagonal prism are of equal length, then it is said to be a regular pentagonal prism. In a regular pentagonal prism, all the rectangular faces are congruent. The rectangular faces are said to be lateral when the pentagonal faces of regular pentagonal prism are bases. The lateral side faces are called lateral edges.
Rectangular Pentagonal Prism
A prism is a right pentagonal prism when it has two congruent and parallel pentagonal faces and five rectangular faces that are perpendicular to the triangular ones.
Volume and Surface Area of a Pentagonal Prime
The two important measures made on a pentagonal prism is to find its volume and surface area.
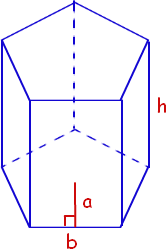
Pentagonal Prism
Volume of Pentagonal Prism Formula
To find the volume of a regular pentagonal prism, first, you have to find the apothem length (a). The apothem length is a measure from the centre of a polygon to the midpoint of any side. The formula to find the volume of a pentagonal prism is given as:
| Volume of pentagonal prism= (5/2)×a×b×h cubic units |
Where,
- a = Apothem length of the pentagonal prism
- b = Base length of the pentagonal prism
- h = Height of the pentagonal prism
Learn More: Volume of a Prism
Surface Area of Pentagonal Prism Formula
The surface area is the area that describes the material that will be used to cover a geometric solid shape. The formula to find the surface area of the pentagonal prism is given by:
| Surface area of pentagonal prism = 5ab + 5bh square units |
Where,
- a = apothem length of the pentagonal prism
- b = base length of the pentagonal prism
- h = height of the pentagonal prism
Learn More: Area Of a Prism
Example Question Based on Pentagonal Prism Formulas
Question: Find the surface area and volume of the pentagonal prism with apothem length of 6 cm, base length of 10 cm and height of 11 cm?
Solution:
Given,
Apothem Length of the pentagonal prism, a = 6 cm
Base length of the pentagonal prism, b = 10 cm
Height of the pentagonal prism, h = 11 cm
Volume and the surface area of a pentagonal prism
Volume of the pentagonal prism = (5/2)abh cu.units
= 5/2 × (6×10×11)
= 5/2 × (660)
= 5 × 330
= 1650
Therefore, the volume of the pentagonal prism is 1650 cm3
Surface area of pentagonal prism = 5ab + 5bh square units
= 5 (6×10) + 5 (10×11)
= 5(60) + 5(110)
= 300 + 550
= 850
Therefore, the surface area of pentagonal prism is 850 cm2 .
More Topics Related to Prisms
| Prism Formula | Three Dimensional Shapes |
| Triangular Prism | Rectangular Prism |
| Square Prism | Three Dimensional Shapes |
Frequently Asked Questions
What is Prism?
A prism can be defined as a three-dimensional shape which consists of two parallel, congruent faces called bases.
What is a Pentagonal Prism?
A pentagonal prism can be defined as a prism having two pentagonal bases and five rectangular sides.
What is the Formula for Surface Area of a Pentagonal Prism?
The surface area of a pentagonal can be found out using the following formula:
A = 5ab + 5bh
What is the Formula for Volume of a Pentagonal Prism?
The volume of a pentagonal prism can be calculated using the following formula:
V = (5/2)×a×b×h