Have you ever walked around the corner (or edge) of a park? After completion of a whole round, the distance travelled by you will be exactly equal to the perimeter of a figure.

Therefore, the total distance around the outside of a polygon is known as the Perimeter of a polygon. A polygon is a 2-dimensional figure, but the perimeter is a one-dimensional measurement. It is the measurement of the path that surrounds a two-dimensional shape. In this article, we are going to discuss the perimeter of different polygons such as triangle, square, rectangle with formulas and examples.

How to Find the Perimeter of a Polygon?

From the definition of a perimeter, the perimeter is defined as the sum of the length of each side. Consider for an example, a quadrilateral whose sides are 12, 6, 8 and 9, the perimeter is given by:

Perimeter = 12 + 6 + 7 + 9 = 34

For a Regular polygon, which has all the sides of equal length, the perimeter is defined as,

Perimeter = n.s Units 

where n = number of sides of a polygon,
and s = length of a side

Perimeter of a Triangle

Imagine that you are asked to find the perimeter of the triangle given in the following figure.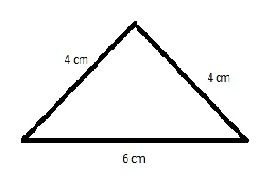

If perimeter is the length of the complete boundary of some surface, then individual side lengths should add up to give us the perimeter. Therefore the perimeter of the triangle given above can be calculated as follows.

= 4 cm + 4 cm + 6 cm

= 14cm

Therefore, the perimeter of the above triangle is 14 cm.

Perimeter of a Square

What if you had to find the perimeter of a square in the image below?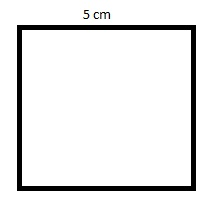

The only information we have regarding the figure above is that it is a square and it has a single side length of 5 cm. But in a square, all four sides are of equal length. Therefore, the perimeter of this square can be calculated as follows.

Method 1: Perimeter: 5 cm + 5 cm + 5 cm + 5 cm

= 4 x 5 cm

= 20 cm

Method 2: As we know, a square is a regular type of a polygon, therefore

Perimeter = n.s

= 4 \(\times \)   5

= 20 cm

Since all squares have the property where all sides are equal, we can generalize a formula for the perimeter of a square.

The perimeter of a square = 4a

where,

a is the length of a side in the square

Perimeter of a Rectangle

A rectangle depicted in the image below has been given to you.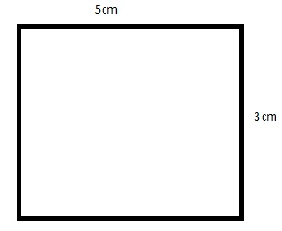

You are asked to find the perimeter of the rectangle and two of the side lengths are given to you. We already know that in a rectangle, the opposite side is equal to each other in length. So the perimeter of this rectangle can be calculated as follows.

5 cm + 5 cm + 3 cm + 3 cm

= (2 x 5 cm) + (2 x 3 cm)

= 2 x (5 + 3)

= 16 cm

The formula for calculating the perimeter of a rectangle can, therefore, be generalised as follows.

Perimeter of a rectangle = 2 x (l + b)

where,

l is the length of the rectangle

b is the breadth of the rectangle

For more articles in Mathematics, log onto www.byjus.com.To watch interesting videos on the topic, download BYJU’S- The Learning App.