The integration of a function f(x) is given by F(x) and it is given as:

∫f(x)dx = F(x) + C

Here R.H.S. of the equation means integral of f(x) with respect to x.

F(x)is called anti-derivative or primitive.

f(x)is called the integrand.

dx is called the integrating agent.

C is an arbitrary constant called as the constant of integration.

x is the variable of integration.

The anti-derivatives of basic functions are known to us. The integrals of these functions can be obtained readily. In the upcoming discussion let us discuss few important formulae and their applications in determining the integral value of other functions.

Integration Formulas and Proofs

1.

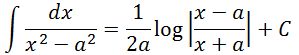
Proof: The integrand can be expressed as:

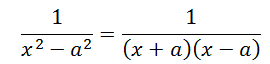
Multiplying the numerator and the denominator by 2a and simplifying the obtained expression we have;

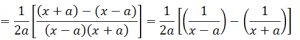
Therefore, upon integrating the obtained expression with respect to x, we have;

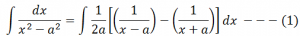
According to the properties of integration, the integral of sum of two functions is equal to the sum of integrals of the given functions, i.e.,

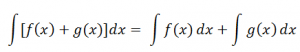
Therefore equation 1 can be rewritten as:

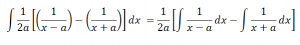
Integrating with respect to x, we have

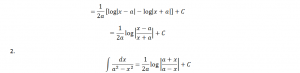
Proof: The integrand can be expressed as:

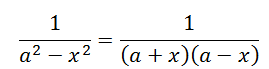
Multiplying the numerator and the denominator by 2a and simplifying the obtained expression we have;

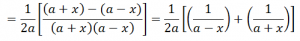
Therefore, upon integrating the obtained expression with respect to x, we have;

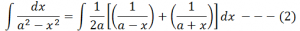
According to the properties of integration, the integral of sum of two functions is equal to the sum of integrals of the given functions, i.e.,

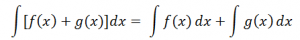
Therefore equation 2 can be rewritten as:

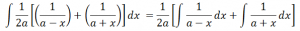
Integrating with respect to x, we have

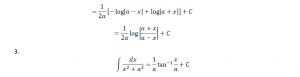
Proof: Let x = a tan Ɵ. Differentiating both sides of this equation with respect to x we have;

dx = a sec²Ɵ dƟ

Therefore, using this, the integral can be expressed as:

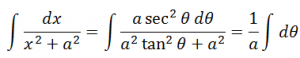
Integrating with respect to x, we have

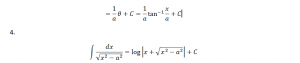
Proof: Let x = a sec Ɵ. Differentiating both sides of this equation with respect to x we have;

dx = a secƟ tan Ɵ dƟ

Therefore, using this, the integral can be expressed as:

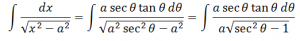
Using the trigonometric identity sec²Ɵ– 1 = tan²Ɵ, the above equation can be written as

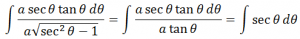
Integrating with respect to x, we have

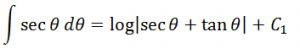
Substituting the value of Ɵ in the above equation we have;

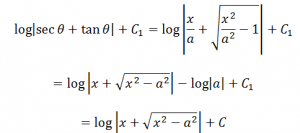
Here, C = C₁ – log |a|

5.

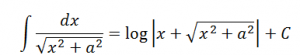
Proof: Let x = a tan Ɵ. Differentiating both sides of this equation with respect to x we have;

dx = a sec² Ɵ dƟ

Therefore, using this, the integral can be expressed as:

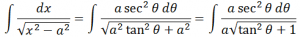
Using the trigonometric identity sec²Ɵ = 1 + tan²Ɵ, the above equation can be written as

Integrating with respect to x, we have

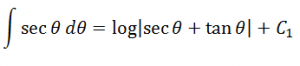
Substituting the value of Ɵ in the above equation we have;

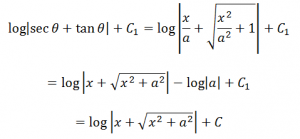
Here, C = C₁ – log |a|

6.   

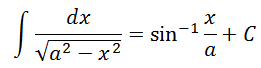
Proof: Let x = a sin Ɵ. Differentiating both sides of this equation with respect to x we have;

dx = a cosƟ dƟ

Therefore, using this, the integral can be expressed as:

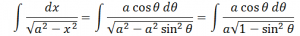
Using the trigonometric identity 1 – sin²Ɵ =cos²Ɵ, the above equation can be written as

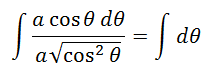
Integrating with respect to x, we have

Substituting the value of Ɵ in the above equation we have;

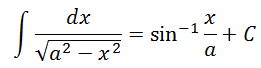
To learn more about integration download BYJU’S- The Learning App.