Quadrant
A quadrant is a region defined by the two axes (x-axis and y-axis) of the coordinate system. When the two axes, x-axis and y-axis, intersect each other at 90 degrees, the four regions so formed are the quadrants. These regions include both positive and negative values of x-axis and y-axis, called coordinates. The coordinates represent the position of a point in a quadrant.
What is a Quadrant?
The axes (x-axis and y-axis) of a two-dimensional Cartesian plane system divides the plane into four infinite regions called quadrants. The horizontal line or x-axis and vertical line or y-axis intersect each other at the right angle. The intersection of two lines is known to be the reference point. All the measurement is done taking this point as the reference (or starting point) in the coordinate system.
A quadrant is simply defined as the region of a cartesian plane formed when the x-axis and y-axis intersect each other.
Four Quadrants in Coordinate Plane
Well, the graph is divided into sections or four quadrants, based on those values.
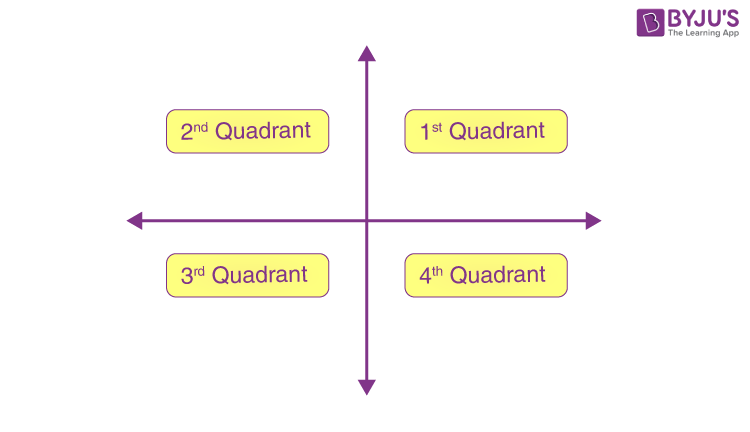
1st Quadrant: The upper right-hand corner of the graph is the first quadrant. In this quadrant the values of x and y both are positive.
2nd Quadrant: The upper left-hand corner of the graph is the second quadrant. In this quadrant, the value of x is negative whereas the value of y is positive.
3rd Quadrant: The lower left-hand corner of the graph is the third quadrant. It contains the negative values of both x and y.
4th Quadrant: Finally, the fourth quarter is at the lower right-hand corner, which has a positive value of x and negative values of y.
Sign Convention in Quadrants
If we observe the XY plane, when we from left to right, the value of x on the horizontal line or x-axis, increases. Similarly, in case of y-axis, the value of y increases, when we move from down to up. Since the plane is divided into four quadrants, then the point on each quadrant will have different signs of x and y.
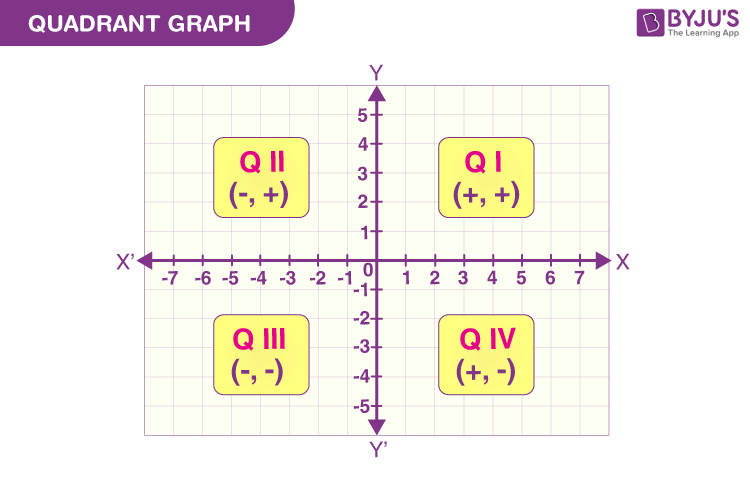
| Quadrants | x-coordinate | y-coordinate |
| 1st Quadrant | Positive (+) | Positive (+) |
| 2nd Quadrant | Negative (-) | Positive (+) |
| 3rd Quadrant | Negative (-) | Negative (-) |
| 4th Quadrant | Positive (+) | Negative (-) |
Thus, from the above table we can state:
- point of 1st quadrant will have a positive value of both x and y
- point of 2nd quadrant will have a negative value of x and a positive value of y
- point of 3rd quadrant will have both negative values of x and y
- point of 4th quadrant will have a positive value of x and a negative value of y
Check the quadrant graph below for a better understanding.
What is Origin?
The origin is the point of intersection of the x-axis and y-axis in a cartesian plane. Origin is represented by the point (0,0). Hence, the values of x and y at origin are equal to 0.
Plotting Points on Quadrants
As we know, in a cartesian plane, the points are defined by the x-axis and y-axis. The points are represented by the ordered pair (x, y), where x is the x-coordinate (also called abscissa) and y is the y-coordinate (also called ordinate). To plot the point in a quadrant, we need to check the sign of these coordinates. The coordinates x and y will represent the distance of the point from the x-axis and y-axis, respectively.
For example, we need to plot a point (-3, 4) in the cartesian plane. By the signs of coordinates of the point, we can observe, the point is the 2nd quadrant. Hence, it will be at a distance of 3 from the x-axis and 4 from the y-axis, taking origin as a reference point.
Trigonometric values in Different Quadrants
| Trigonometric Function | 1st Quadrant | 2nd Quadrant | 3rd Quadrant | 4th Quadrant |
| Sin | +ve | +ve | -ve | -ve |
| Cos | +ve | -ve | -ve | +ve |
| Tan | +ve | -ve | +ve | -ve |
| Cot | +ve | -ve | +ve | -ve |
| Sec | +ve | -ve | -ve | +ve |
| Cosec | +ve | +ve | -ve | -ve |
Related Articles
- Area Of Quadrant
- Coordinate Geometry Formulas
- Polar Coordinate System
- Cartesian Plane
- Cartesian Product And Ordered Pairs
Solved Examples on Quadrant
Q.1: Check and answer to which quadrants do the given points lie?
- (1, 4)
- (-3, -5)
- (-2, 6)
- (7, -4)
Solution: Since, the coordinates of (1, 4) are both positive, thus it lies on the 1st quadrant.
The coordinates of the point (-3, -5) are both negative, thus it lies on the 3rd quadrant.
The coordinates of the point (-2, 6) are negative on x-axis and positive on y-axis, thus it lies on 2nd quadrant.
The coordinate of the point (7, -4) are positive on x-axis and negative on y-axis, thus it lies on 4th quadrant.
Q.2: Give an example of a point that lies on the third quadrant.
Solution: In the third quadrant, the coordinates of the x-axis and y-axis are both negative. (-1, -3) is an example of a point in the third quadrant.
Q.3: Where does the point (-4, 0) lie in the cartesian plane? Does it lie in a quadrant?
Solution: The point (-4, 0) lies on the horizontal axis or x-axis, which is at a distance of 4 units from the origin. It does not lie in any quadrant.
Practice Questions
- Plot the point (-2.5, 7) and explain which quadrant does it lies.
- Give examples of points that lie in each quadrant.
- Where does the point (0, 5) lie in the coordinate plane?
Frequently Asked Questions – FAQs
What is a quadrant?
What is the intersection of two axes called?
What are the four quadrants?
Which quadrant has both the values of coordinates positive?
To learn more about math-related articles, visit BYJU’S -The Learning App.