Relations and Functions Worksheet

Trigonometry

Trigonometry Logo

Relations and Functions Worksheet

Home → Relations and Functions Worksheet

What is the Relation?

Relations can be described as a set of ordered pairs. Let’s look at some examples of relation, such as:

  • {(1,0) , (25,50)}
  • {(Mon, Sun), (Tue, Sat)}

Where { } denotes the set symbol.

A relation is a correspondence among two or sets (known as the domain and range) such that there are one or more elements assigned to every element or member of the domain.

Example 1

(2, 4), (2, 3), (3, 7), (5, 2) is a relation of

Domain {2, 3, 5}

Range {2, 3, 4, 7}

What is Function?

A relation “f” from set “X” to set “y” is said to be a function, if every element of set X has only one image in set Y. The function is symbolically represented as  f : X →Y. It means that the f is a function from set X to set Y , X is called the domain of function “f’ and Y is called the codoamin of the function “f”.

Worksheet on Relations and Functions

Solve the problems on relations and functions given below:

Determine the domain and range of the given functions:

{17, -9), (10, -5), (8, 3), (8, 4), (6, -14)}

Range =_____

Domain = _____

{(5, 5), (3,8), (5,4), (7,5), (13, 8), (6, 2)}

Range = _____

Domain = _____
Find the domain and range value from the given tabular form:

x y
-18 11
-16 11
-10 11
-8 11
3 11
7 11
Evaluate the range for the given domain and the function.

  1. If  the function is f(x)= 6x-27, and the domain is {-5, 3, 15, 17}, then find the range.
  2. Calculate the range for the function f(x)= (3x-2)/5, if its domain is {-6, -1, 4, 9, 19}
Write the domain and range for the given function:

  1. f(x)= -|3x-7|
  2. f(x) = 4/(x+1)
  3. f(x)= 4x2 – 2
Check whether the set of ordered pair represent the function, and state true or false.

  1. {(12, -18), (15, 1), (12, 5), (0, 9), (-5, -17)} – _____
  2. {(15, -3), (-6, 9), (-3, 0), (-1, 16)} – _____
Check that the given equation represents the function and state true or false.

  1. 9y9 = 11+8x
  2. 4x4 = y2
Which of the given function represents a function?

(a) 4+3x = y8  (b) y5 = -12-x   (c) -2y6=-5+9x  (d)(7x2+15)/4 = y2
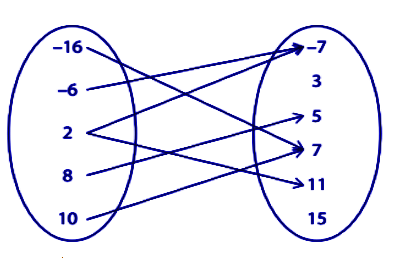
Find the domain and range for the given relation:

     Domain = _____

     Range = _____
Which of the following statement is true:

  1. All the relations are functions.
  2. In every relation, each input value has exactly one output value.
  3. A relation is defined as a set of input and output values which are related in some way.
  4. All the above-given statements are true.