Right Angle
A right angle is an angle that is exactly equal to 90 degrees (or π/2) in measure. We can see many real-life examples of the right angles in our daily life. For example, the corner of a book, edges of the cardboard, etc. Any shape that is a square or a rectangle, will have its corners equal to 90 degrees or right angle. A right angle is hence called a 90-degree angle.
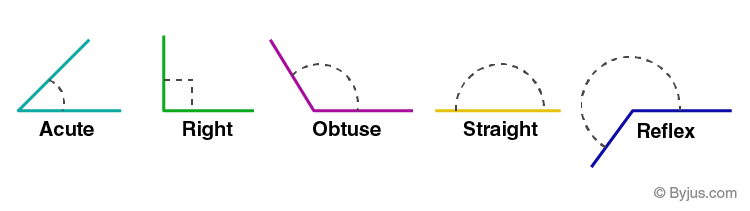
In geometry, the figure formed by two rays, called the sides of the angle, sharing a common endpoint, called the vertex of the angle is known as an angle. Angles created by two rays lie in the plane that contains the rays. The intersection of two planes also forms angles. The angle is also used to designate the measure of an angle or a rotation. Based on this rotation, various types of angles are defined. In this article, you will learn one of these angles, along with examples in detail.
| Table of Contents: |
What is a Right Angle?
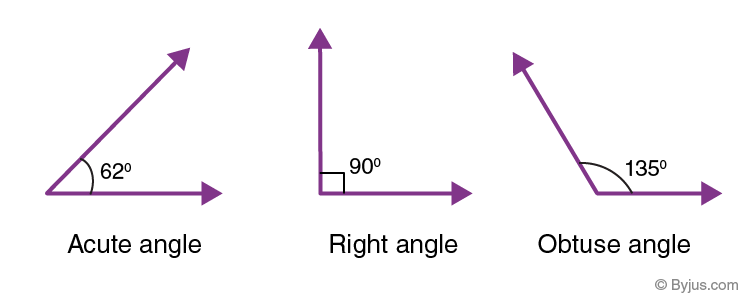
If the measure of the angle between two rays is exactly equal to 90 degrees or π/2, then the angle is called a right angle. Angles that measure less than 90° such as 87°, 56°, 77°, 42°, etc., are acute angles and the angles which measure more than 90° such as 91°, 98°, 102°, 150°, 167°, etc., are called obtuse angles.
The measure of right angle can be written in terms of degrees as 90° and in terms of radians as π/2 (= 1.5708) radians.
Right Angle Shape
Below figure shows the shape of a right angle formed by two rays. It looks like the alphabet ‘L’.
In the same way, we can see a few examples around us in real life, that have a right angle shape.
- Corners of a wall
- L-shapes Sofas
- Edges of windows and doors
- Corners of laptops
Right Angle Triangle
A right-angled triangle is one that has three sides, “base” “hypotenuse” and “perpendicular” with the angle between the base and the perpendicular is 90°. A right-angled triangle is one of the basic shapes in geometry and it forms the foundation for trigonometry.
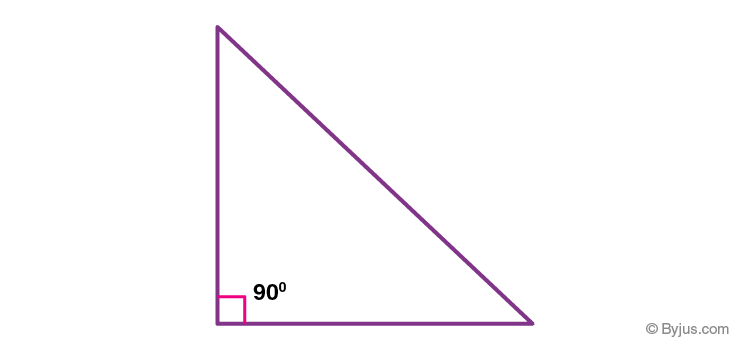
In the right triangle, the hypotenuse is the longest side and is opposite the right angle of the triangle.
Right Angle Triangle Formula
The formula used to determine whether the given triangle is the right triangle or not is the Pythagoras theorem. The theorem states that the square of the hypotenuse is equal to the sum of the squares of the other two sides.
(Hypotenuse)2 = (Base)2 + (Perpendicular)2
Click here to learn more about the Pythagoras theorem formula in maths.
Right Angle Triangle Properties
Some of the important properties of a right triangle are listed below.
- A right triangle has one angle exactly equal to 90 degrees
- The angles other than the right angle must be acute angles, i.e. less than 90 degrees
- The side opposite to vertex of 90 degrees is called the hypotenuse of the right triangle and is the longest side of the triangle
- The other two sides adjacent to the right angle are called base and perpendicular.
- The circumcircle of the right triangle passes through all three vertices, and the radius of this circle is equal to half of the length of the hypotenuse.
Right Angle Triangle Area
The area of a triangle is the area enclosed by three sides of the triangle in a plane. The formula to find the area of a right triangle is given by:
Area (A) = = ½ × Base × Height
Here,
Height = Perpendicular
Right Angle Isosceles Triangle
When the two sides other than hypotenuse, i.e. base and perpendicular are congruent in a right triangle, then it is called a right angle isosceles triangle or simply isosceles right triangle. In this type of triangle, the angles made by the base and perpendicular with the hypotenuse are congruent, i.e. both measure 45 degrees each.
Right Angle Examples
We may observe right angles in many objects such as edges of a book meeting at right angles at the vertices, sides of a rectangular table or boards in classrooms forming right angles at the corners. Below figure shows the rectangular board that has right angles at its corners.

We know that all the interior angles of a square are right angles, i.e. equal to 90 degrees as shown in the figure.
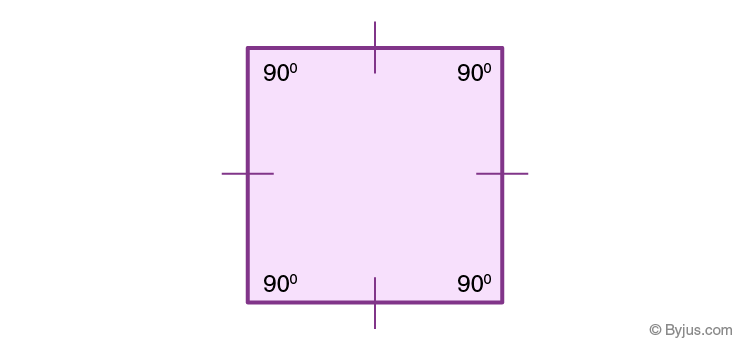
Also, the angle formed by the x-axis and y-axis in the coordinate plane at the center (intersection of axes) is right angles.
Related Articles
Frequently Asked Questions on Right Angle
How do you define a right angle?
A right angle is defined as the angle made by two rays at a vertex exactly equal to 90 degrees. That means, both the rays are perpendicular to each other.
What is an example of a right angle?
There are many real-life examples that contain right angles such as corners of notebooks, tables, boards in classrooms, doors and windows of a house, which have their corners in the shape of a right angle, and so on.
Why is it called a right angle?
A right-angle is so-called a right angle since this angle forms when two rays (lines or line segments) intersect each other at 90 degrees or when they are perpendicular to each other.
What are the 3 angles of a right triangle?
In a right triangle, the three angles include one right angle and two acute angles since the sum of all the interior angles of any triangle must be 180 degrees. Hence, a right triangle has two acute angles other than the right angle.
What is the formula of the right angle triangle?
If a, b, c are the sides of a triangle such that a being the longest side and b, c are the perpendicular sides, then a2 + b2 = c2.
This is called the formula of a right-angled triangle as it helps in determining whether the given three sides belong to the right triangle or not.