Sin Cos Tan Values
In trigonometry, sin cos and tan values are the primary functions we consider while solving trigonometric problems. These trigonometry values are used to measure the angles and sides of a right-angle triangle. Apart from sine, cosine and tangent values, the other three major values are cotangent, secant and cosecant.
When we find sin cos and tan values for a triangle, we usually consider these angles: 0°, 30°, 45°, 60° and 90°. It is easy to memorise the values for these certain angles. The trigonometric values are about the knowledge of standard angles for a given triangle as per the trigonometric ratios (sine, cosine, tangent, cotangent, secant and cosecant).
Sin Cos Tan Formula
The three ratios, i.e. sine, cosine and tangent have their individual formulas. Suppose, ABC is a right triangle, right-angled at B, as shown in the figure below:
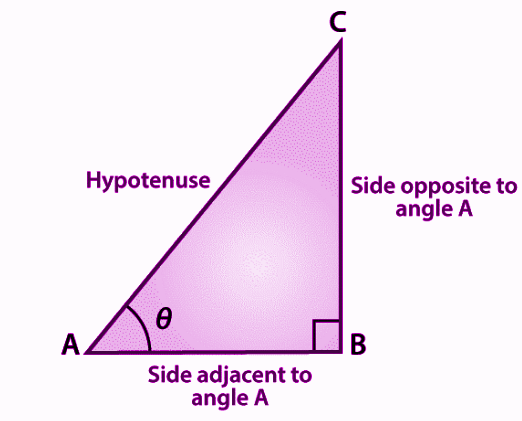
Now as per sine, cosine and tangent formulas, we have here:
- Sine θ = Opposite side/Hypotenuse = BC/AC
- Cos θ = Adjacent side/Hypotenuse = AB/AC
- Tan θ = Opposite side/Adjacent side = BC/AB
We can see clearly from the above formulas, that:
Tan θ = sin θ/cos θ
Now, the formulas for other trigonometry ratios are:
- Cot θ = 1/tan θ = Adjacent side/ Side opposite = AB/BC
- Sec θ = 1/Cos θ = Hypotenuse / Adjacent side = AC / AB
- Cosec θ = 1/Sin θ = Hypotenuse / Side opposite = AC / BC
The other side of representation of trigonometric values formulas are:
- Tan θ = sin θ/cos θ
- Cot θ = cos θ/sin θ
- Sin θ = tan θ/sec θ
- Cos θ = sin θ/tan θ
- Sec θ = tan θ/sin θ
- Cosec θ = sec θ/tan θ
Also, read:
Sin Cos Tan Chart
Let us see the table where the values of sin cos tan sec cosec and tan are provided for the important angles 0°, 30°, 45°, 60° and 90°
| Angles (in degrees) | 0° | 30° | 45° | 60° | 90° |
| Angles (in radian) | 0 | π/6 | π/4 | π/3 | π/2 |
| Sin θ | 0 | 1/2 | 1/√2 | √3/2 | 1 |
| Cos θ | 1 | √3/2 | 1/√2 | 1/2 | 0 |
| Tan θ | 0 | 1/√3 | 1 | √3 | ∞ |
| Cot θ | ∞ | √3 | 1 | 1/√3 | 0 |
| Sec θ | 1 | 2/√3 | √2 | 2 | ∞ |
| Cosec θ | ∞ | 2 | √2 | 2/√3 | 1 |
How to find Sin Cos Tan Values?
To remember the trigonometric values given in the above table, follow the below steps:
- First divide the numbers 0,1,2,3, and 4 by 4 and then take the positive roots of all those numbers.
- Hence, we get the values for sine ratios,i.e., 0, ½, 1/√2, √3/2, and 1 for angles 0°, 30°, 45°, 60° and 90°
- Now, write the values of sine degrees in reverse order to get the values of cosine for the same angles.
- As we know, tan is the ratio of sin and cos, such as tan θ = sin θ/cos θ. Thus, we can get the values of tan ratio for the specific angles.
Sin Values
sin 0° = √(0/4) = 0
sin 30° = √(1/4) = ½
sin 45° = √(2/4) = 1/√2
sin 60° = √3/4 = √3/2
sin 90° = √(4/4) = 1
Cos Values
cos 0° = √(4/4) = 1
cos 30° = √(3/4) = √3/2
cos 45° = √(2/4) = 1/√2
cos 60° = √(1/4) = 1/2
cos 90° = √(0/4) = 0
Tan Values
tan 0° = 0/1 = 0
tan 30° = [(√1/4)/√(3/4)] = 1/√3
tan 45° = √(2/4) = 1/√2
tan 60° = [(√3/2)/(½)] = √3
tan 90° = 1/0 = ∞
Hence, the sin cos tan values are found.