Solving linear equations means to find the solution of a linear equation. Here, the methods of solving linear equations are explained for its three main types which include linear equations in one variable, linear equations in two variables and linear equations in three variables.

What Does Solving Linear Equations Mean?

Solving a linear equation refers to finding the solution of linear equations in one, two, three or variables. In simple words, a solution of a linear equation means the value or values of the variables involved in the equation.

How to Solve Linear Equations?

There are six main methods to solve linear equations. These methods for finding the solution of linear equations are:

• Graphical Method
• Elimination Method
• Substitution Method
• Cross Multiplication Method
• Matrix Method
• Determinants Method

Graphical Method of Solving Linear Equations

To solve linear equations graphically, first graph both equations in the same coordinate system and check for the intersection point in the graph. For example, take two equations as 2x + 3y = 9 and x – y = 3.

Now, to plot the graph, consider x = {0. 1, 2, 3, 4} and solve for y. Once (x, y) is obtained, plot the points on the graph. It should be noted that by having more values of x and y will make the graph more accurate.

Check: Graphical Method of Solving Linear Programming

The graph of 2x + 3y = 9 and x – y = 3 will be as follows:

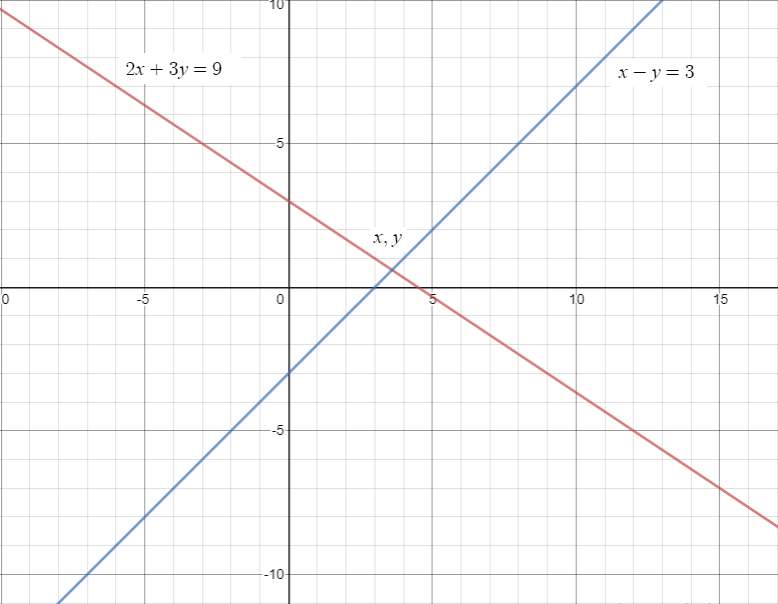
In the graph, check for the intersection point of both the lines. Here, it is mentioned as (x, y). Check the value of that point and that will be the solution of both the given equations. Here, the value of (x, y) = (3.6, 0.6).

Elimination Method of Solving Linear Equations

In the elimination method, any of the coefficients is first equated and eliminated. After elimination, the equations are solved to obtain the other equation. Below is an example of solving linear equations using the elimination method for better understanding.

Consider the same equations as

2x + 3y = 9 ———–(i)

And,

x – y = 3 ———–(ii)

Here, if equation (ii) is multiplied by 2, the coefficient of “x” will become the same and can be subtracted.

So, multiply equation (ii) × 2 and then subtract equation (i)

2x + 3y = 9

(-)

2x – 2y = 6

_____________

-5y = -3

Or, y = ⅗ = 0.6

Now, put the value of y = 0.6 in equation (ii).

So, x – 0.6 = 3

Thus, x = 3.6

In this way, the value of x, y is found to be 3.6 and 0.6.

Substitution Method of Solving Linear Equations

To solve a linear equation using the substitution method, first, isolate the value of one variable from any of the equations. Then, substitute the value of the isolated variable in the second equation and solve it. Take the same equations again for example.

Consider,

2x + 3y = 9 ———–(i)

And,

x – y = 3 ———–(ii)

Now, consider equation (ii) and isolate the variable “x”.

So, equation (ii) becomes,

x = 3 + y.

Now, substitute the value of x in equation (i). So, equation (i) will be-

2x + 3y = 9

⇒ 2(3 + y) + 3y = 9

⇒ 6 + 2y + 3y = 9

Or, y = ⅗ = 0.6

Now, substitute “y” value in equation (ii).

x – y =3

⇒ x = 3 + 0.6

Or, x = 3.6

Thus, (x, y) = (3.6, 0.6).

Cross Multiplication Method of Solving Linear Equations

Linear equations can be easily solved using the cross multiplication method. In this method, the cross-multiplication technique is used to simplify the solution. For the cross-multiplication method for solving 2 variable equation, the formula used is:

x /(b₁ c₂ − b₂ c₁) = y / (c₁ a₂ − c₂ a₁) = 1 /(b₂ a₁ − b₁ a₂)

For example, consider the equations

2x + 3y = 9 ———–(i)

And,

x – y = 3 ———–(ii)

Here,

a₁ = 2, b₁ = 3, c₁ = -9

a₂ = 1, b₂ = -1, c₂ = -3

Now, solve using the aforementioned formula.

x = (b₁ c₂ − b₂ c₁) / (b₂ a₁ − b₁ a₂)

Putting the respective value we get,

x = 18/5 = 3.6

Similarly, solve for y.

y = (c₁ a₂ − c₂ a₁) / (b₂ a₁ − b₁ a₂)

So, y = ⅗ = 0.6

Matrix Method of Solving Linear Equations

Linear equations can also be solved using matrix method. This method is extremely helpful for solving linear equations in two or three variables. Consider three equations as:

a₁x + a₂y + a₃z = d₁

b₁x + b₂y + b₃z = d₂

c₁x + c₂y + c₃z = d₃

These equations can be written as:

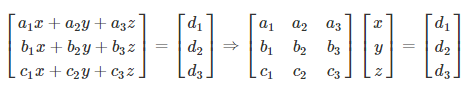
⇒ AX = B ————-(i)

Here, the A matrix, B matrix and X matrix are:

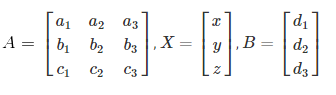
Now, multiply (i) by A^-1 to get:

A⁻¹AX = A⁻¹B ⇒ I.X = A⁻¹B

⇒ X = A⁻¹B

• Learn more on how to solve linear equations with matrix method here.

Determinant Method of Solving Linear Equations (Cramer’s Rule)

Determinants method can be used to solve linear equations in two or three variables easily. For two variables and three variables of linear equations, the procedure is as follows.

For Linear Equations in Two Variables:

x = Δ₁/Δ,

y = Δ₂/Δ

Or, x = (b₁ c₂ − b₂ c₁) / (b₂ a₁ − b₁ a₂) and y = (c₁ a₂ − c₂ a₁) / (b₂ a₁ − b₁ a₂)

Here,

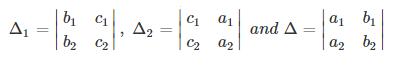
For Linear Equations in Three Variables:

• Learn more on how to solve linear equations with determinants method here.

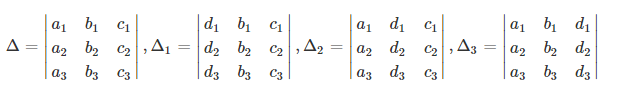
Related Video: Solving an Equation

Methods of Solving Linear Equations in One Variable

Solving a linear equation with one variable is extremely easy and quick. To solve any two equations having only 1 variable, bring all the variable terms on one side and the constants on the other. The graphical method can also be used in which the point of intersection of the line with the x-axis or y-axis will give the solution of the equation.

For example, consider the equation 2x + 4 + 7 = 4x – 3 + x

Here, combine the “x” terms and bring them on one side.

So,

5x – 2x = 14

Or, x = 14/3

Methods of Solving Linear Equations in Two Variables

To solve a linear equation in two variables, any of the above-mentioned methods can be used i.e. graphical method, elimination method, substitution method, cross multiplication method, matrix method, determinants method.

Methods of Solving Linear Equations in Three or More Variables

For solving any equation having three or more variables, the graphical, elimination and the substitution method is not feasible. For solving a three-variable equation, the cross-multiplication method is the most preferred method. Even matrix Cramer’s rule is extremely useful for solving equations having 3 or more variables.

Check: Solve Linear Equation in Two Or Three Variables

Topics Related to Solution of Linear Equations: