Spherical coordinates of the system denoted as (r, θ, Φ) is the coordinate system mainly used in three dimensional systems. In three dimensional space, the spherical coordinate system is used for finding the surface area. These coordinates specify three numbers: radial distance, polar angles and azimuthal angle. These are also called spherical polar coordinates. Cartesian coordinates (x,y,z) are used to determine these coordinates. We will learn the conversion here in this article.

The radius is measured from a fixed origin, the polar angle is measured from an imaginary point near to the exact location and the azimuthal angle on a reference plane passes through the origin. The radial distance is also known as radial coordinate apart from the radius. The polar angle could be mentioned as a colatitude, zenith angle, normal angle, or inclination angle. ‘r’ is the radius of the system, ‘θ’ is an inclination angle and ‘Φ’ is azimuth angle.

Now let us understand the conversion of rectangular coordinates to spherical coordinates and vice-versa with the help of examples.

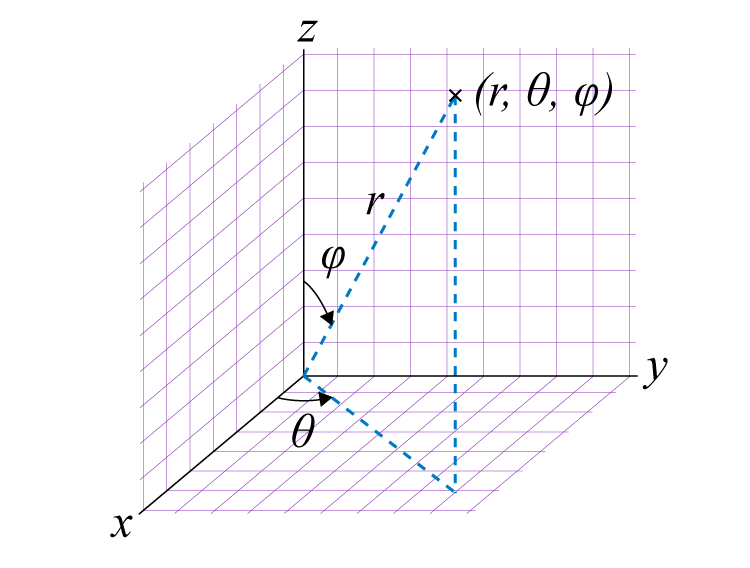
Converting Rectangular to Spherical coordinates

For a three dimensional plane having coordinates (r, θ, Φ) in x, y and z plane, respectively, the values of these coordinates can be estimated as;

Let us see an example to check how to convert rectangular coordinates to spherical:

Example: Convert the rectangular coordinates (21, 28, 32) into spherical coordinates.

Solution: Given x = 21, y = 28, z = 32

Formula:

r = √ (x² + y² + z²)

θ = cos^-1(x / r)

Φ = cos^-1 (x / (r * sin θ))

Substitute the given x, y, z values in the given formula, we get;

r = √ (21² + 28² + 32²)

r = 47.42

θ = cos^-1(x / r)

= cos^-1(21 / 47.42)

= 63.71°

Φ = cos^-1 (x / (r * sin θ)

= cos^-1 (21 / (47.42 * sin 63.71°))

= 60.42°

Therefore, the required coordinates are 47.42, 63.71°, 60.42°.

Converting Spherical to Rectangular Coordinates

To convert spherical to rectangular coordinates we need to use the below formulas:

Below is an example to understand the conversion better.

Example: Convert the spherical coordinates (32, 68°, 74°) into rectangular coordinates

Solution: Given spherical coordinates are, r = 32, θ = 68°, Φ = 74°

Convert the above values into rectangular coordinates using the formula,

x = r (sin θ) (cos Φ)

y = r (sin θ) (sin Φ)

z = r (cos θ)

Substitute the above values in the given formulas, we get

x = 32 * (sin 68°) (cos 74°)

x = 8.17

y = 32 * (sin 68°) (sin 74°)

y = 28.51

z = 32 cos 68°

z = 11.98

Therefore, the rectangular coordinates are x = 8.17, y = 28.51, z = 11.98

Practice Problems

Q 1: Convert the spherical coordinates (12, 45°, 60°) into rectangular coordinates.

Q 2: Convert these coordinates (6, 30°, 65°) into rectangular coordinates.

Q 3: Convert the rectangular coordinates (7, 12, 4) into spherical one.

Answers:

1. x = 4.24, y = 7.34, z = 8.48
2. x =1.26, y = 2.7, z = 5.19
3. (14.45, 61.02°, 56.37 )