Surface Area of a Hemisphere
In mathematics, two-dimensional geometry deals with the x-y plane. The extension of 2D geometry is the three-dimensional geometry which deals with three axes, namely x, y and z in the cartesian plane. 3D shapes have three different dimensions like length, breadth and height.
We have learned different types of three-dimensional shapes. In general, the three-dimensional objects are obtained by rotating the two-dimensional objects. Our earth is one of the best examples of 3D shapes, which is spherical in shape. The sphere is obtained from the rotation of 2D shape called the circle.
Hemisphere Definition
A sphere is a three-dimensional solid where all the points lying on the surface is equidistant from the centre. A hemisphere is formed when the plane cuts the sphere into two equal halves. A sphere is a combination of the two hemispheres.
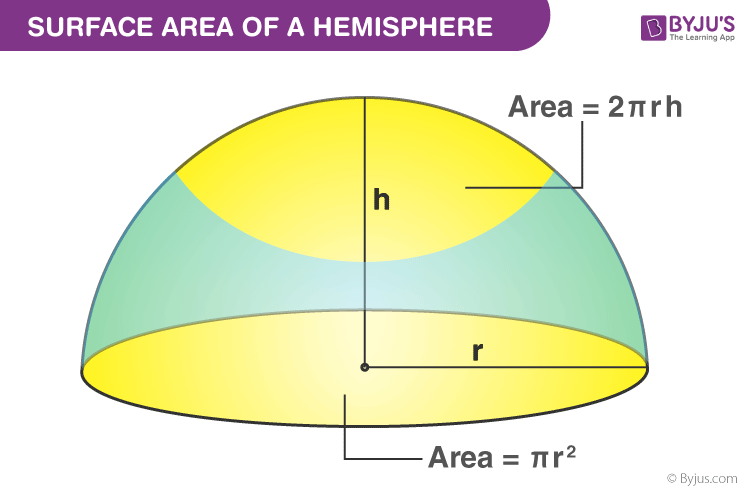
Hemisphere Surface Area
We can easily find the surface area of a hemisphere since the base of the sphere is circular in shape. Generally, there are two different types of surface area. One is the total surface area, and the other is the curved surface area.
Curved Surface Area: The area of the outer surface of the hemisphere is called the curved surface area.
Total Surface Area: The area of the curved surface and the area of the circle (base) is called the total surface area
From the surface area of a sphere, we can easily calculate the surface area of the hemisphere.
Since hemisphere is half of the sphere
CSA of hemisphere = (1/2)surface area of the sphere
CSA = (1/2)4πr2
CSA = 2πr2
The curved surface area of a hemisphere = 2πr2 square units.
The total surface area of the sphere = Curved surface area of sphere + base area
We know that the base of the hemisphere is circular in shape, use the area of the circle.
TSA = 2πr2 + πr2 = 3πr2
Therefore,
The total surface area of a hemisphere = 3πr2 square units
Where π is a constant whose value is equal to 3.14 approximately.
“r” is the radius of the hemisphere.
Solved Problem
The sample problem on hemisphere is given below
Question:
Find the surface area of a hemisphere whose radius is 4 cm?
Solution:
Given:
Radius, r = 4 cm
The curved surface area = 2πr2 square units.
The total surface area = 3πr2 square units
Substitute the value of r in the formula.
(i) CSA of the hemisphere= 2 × 3.14 × 4 × 4
CSA = 3.14 × 32
CSA = 100.48 cm2
(ii) TSA of the hemisphere = 3 × 3.14 × 4 × 4
TSA = 3.14 × 48
TSA = 150.72 cm2
Therefore, the curved and the total surface area of the hemisphere are 100.48 and 150.72 cm2, respectively.
Stay tuned with BYJU’S – The Learning App for many similar topics like volume and surface area of solid shapes and also watch videos to learn with ease in an engaging way.