Surface Integral
In Mathematics, the surface integral is used to add a bunch of values associated with the points on the surface. The computation of surface integral is similar to the computation of the surface area using the double integral except the function inside the integrals. In this article, let us discuss the definition of the surface integral, formulas, surface integrals of a scalar field and vector field, examples in detail.
Surface Integral Definition
In Vector Calculus, the surface integral is the generalization of multiple integrals to integration over the surfaces. Sometimes, the surface integral can be thought of the double integral. For any given surface, we can integrate over surface either in the scalar field or the vector field. In the scalar field, the function returns the scalar value, and in the vector field, the function returns the vector value. Like the line integrals, the surface integrals are of two types, namely:
- Surface Integral of Scalar Function
- Surface Integral of Vector Function
The surface integral of the scalar function is the simple generalisation of the double integral, whereas the surface integral of the vector functions plays a vital part in the fundamental theorem of calculus.
Surface Integral Formula
The formulas for the surface integrals of scalar and vector fields are as follows:
Surface Integral of Scalar Field
Let us assume a surface S, and a scalar function f(x,y, z).
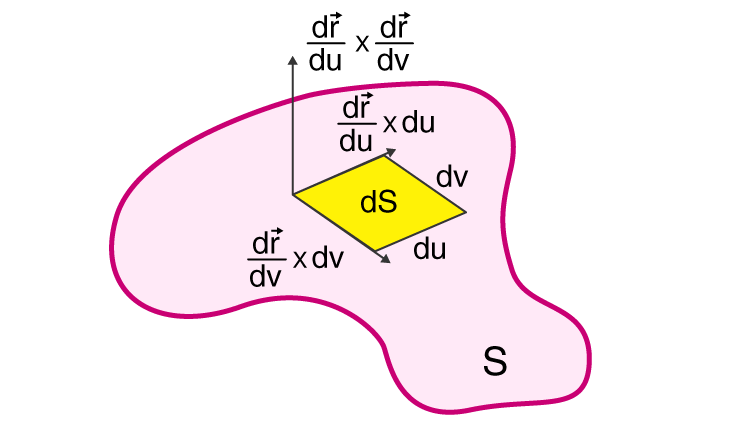
Let S be denoted by the position vector, r (u, v) = x(u, v)i + y(u, v)j + z (u, v)k, then the surface integral of the scalar function is defined as:
Where,
(u, v) are the range of coordinates over the domain of the uv- plane
The absolute value \(\left | \frac{\partial r}{\partial u}\times \frac{\partial r}{\partial v} \right |\) is called the area element
Surface Integral of Vector Field
Let us assume a vector field with function F(x, y, z) and surface S, and it is continuously defined by the position vector r (u, v) = x(u, v)i + y(u, v)j + z (u, v)k.
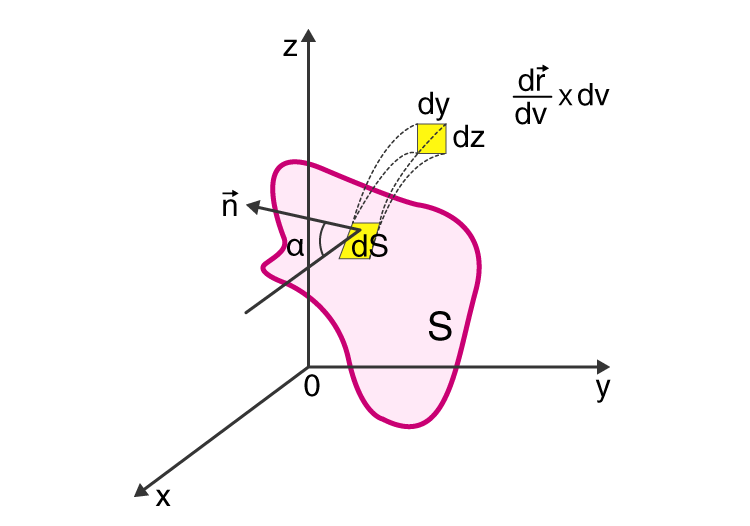
Let n (x, y, z) be a normal unit vector to the surface S at the point (x, y, z), in which the surface S is smooth the vector function n(x, y, z) is continuous, then the unit normal vector has two possibilities such as n(x, y, z) and -n(x, y, z).
If the choice of vector is made, then the surface is oriented. The surface oriented in the vector field may be either outward or inward.
- If the surface “S” oriented is outward, then the surface integral of the vector field is given as:
- If the surface “S” oriented is inward, then the surface integral of the vector field is given as:
Where dS = ndS is known as the vector element of the surface.
Applications of Surface Integrals
The surface integrals are applied in different areas of Science and Engineering.
Some of the applications of the surface integrals in vector calculus are as follows:
- Surface Integrals are used to determine pressure and gravitational force
- In Gauss’ Law of Electrostatistics, it is used to compute the electric field
- To find the mass of the shell
- It is used to calculate the moment of inertia and the centre of mass of the shell
- It helps to determine the electric charge distributed over the surface
Surface Integral Example
An example of computing the surface integrals is given below:
Example:
Solution:
Given: \(\iint_{S}xyz dS\), and z= 1+2x+3y.
=\(\int_{0}^{3}\int_{0}^{2}xy(1+2x+3y)\sqrt{(2)^{2}+(3)^{2}+1}dy dx\)
=\(\int_{0}^{3}\int_{0}^{2}xy+2x^{2}y+3xy^{2}\sqrt{14}dy dx\)
=\(\sqrt{14}\int_{0}^{3}[\frac{xy^{2}}{2}+\frac{2x^{2}y^{2}}{2}+\frac{3xy^{3}}{3}]_{0}^{3} dx\)
Now substitute the limits, we get
Differentiate with respect to x, we get
=\(\sqrt{14}[\frac{2x^{2}}{2}+\frac{4x^{3}}{3}+\frac{8x^{2}}{2}]_{0}^{3}\)
Now substitute the limits,
=\(\sqrt{14}(9+36+36)\)
= \(81 \sqrt{14}\)
=\(9^{2}\sqrt{14}\)
Therefore, the surface integral for the given function is \(9^{2}\sqrt{14}\).
Visit BYJU’S -The Learning App to learn more on Calculus and download the app to learn with ease.