You might already have come across the term vector. A quantity which has magnitude, as well as direction, is represented by a vector. The most common example of a vector in mathematics is a directed line segment. Let us say that a line AB, 5 cm in length, is pointed towards the south. In this case, AB is a vector.

In Maths, there are different types of vectors. Basic mathematical operations can be applied to them as well. In this article, we will talk about a vector which joins two points.

Equation of Vectors Joining Two Point

We can represent a point by its x coordinate, y coordinate and z coordinate. Let us say there are two points represented by their x-, y- and z- coordinates as:

• P1(x₁,y₁,z₁)
• P2(x₂,y₂,z₂)

We join the points P₁ and P₂ by a vector and call it as P₁P₂.

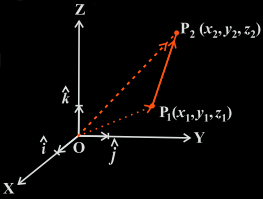
We represent the vectors from the origin O along the x-, y- and z-axes as i, j and k respectively. Now we join the origin O to P₁ with the vector OP₁ and to P₂ with the vector OP₂. Using the triangle law, we get:

\(\overrightarrow{OP_{1}}+ \overrightarrow{P_{1}P_{2}} = \overrightarrow{OP_{2}}\)

Or

\(\overrightarrow{P_{1}P_{2}} = \overrightarrow{OP_{2}}- \overrightarrow{OP_{1}}\)

That is,

\(\overrightarrow{P_{1}P_{2}} = (x_{2}\hat{i} + y_{2}\hat{j}+ z_{2}\hat{k}) – (x_{1}\hat{i} + y_{1}\hat{j}+ z_{1}\hat{k})\)

\(= (x_{2} – x_{1})\hat{i} + (y_{2} – y_{1} ) \hat{j}+ (z_{2}- z_{1})\hat{k}\)

Thus, the above equation represents the vector P₁P₂. Its magnitude can be given by:

\(\overrightarrow{P_{1}P_{2}} = \sqrt{(x_{2}- x_{1})^{2} + (y_{2}- y_{1})^{2} + (z_{2}- z_{1})^{2}}\)

Solved Examples

Question 1: Find the vector and its magnitude which joins the point A with coordinates (4, 5, 6) to point B with coordinates (10, 11, 12).

Solution: The vector is directed from the point A to B and can be denoted by \(\overrightarrow{AB}\)

Thus,

\(\overrightarrow{AB} = (10 – 4) \hat{i} + (11 – 5) \hat{j} + (12 – 6) \hat{k} = 6 \hat{i} + 6 \hat{j} + 6 \hat{k}\)

Magnitude can be given by:

\(\vec{AB}=\sqrt{6^2+6^2+6^2}=\sqrt{36+36+36}=\sqrt{108}=10.39\)

Question 2: Find the vector joining the points P(1, 2, 3) and Q(6, 5, 4) directed to Q from P.

Solution:

The vector which is directed from the point P to Q can be written as \(\vec{PQ}\)

Therefore,

\(\vec{PQ}=(6-1)\hat{i}+(5-2)\hat{j}+(4-3)\hat{k}\\=5\hat{i}+3\hat{j}+\hat{k}\)

To learn more about vectors, section formula and other vector concepts with illustrative examples, by watching interactive video lectures on them, download BYJU’S – The Learning App.