What Are Quadrilaterals?
Quadrilaterals are a two-dimensional plane figure, which has four edges and four vertices. The sides of the quadrilaterals are straight lines and joint with each other end to end. The word ‘quad’ states as four. It is nothing but a polygon which has four corners and four sides. These quadrilaterals can be seen in different shapes, regular or irregular. The examples are a kite, a deck of cards, etc. We will learn the types of quadrilaterals here.
Properties of Quadrilaterals
It has four sides, four corners/vertices and four angles
It has both regular and irregular shape
Total of all its interior angles is equal to 360 degrees
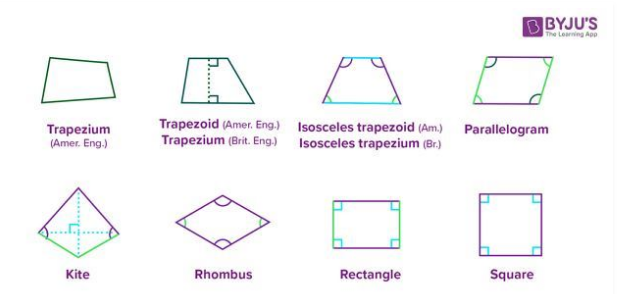
Types of Quadrilaterals
There are various types of quadrilaterals, such as:
Trapezium: One of the opposite sides are parallel
Parallelogram: Both the opposite sides are parallel and equal in length.
Squares: All the sides are equal and the angles are at 90 degrees.
Rectangle: Opposite sides are equal and the angles are at 90 degrees.
Rhombus: All the sides are equal and diagonals bisect at 90 degrees.
Kite: Two pairs of adjacent/neighbouring sides are of equal length.
Quadrilaterals Formulas
Area of Quadrilateral: The region occupied by any type of the quadrilateral in a two-dimensional plane is its area. The formulas for different types of quadrilaterals are given by:
| Area of a Parallelogram | Base x Height |
| Area of a Rectangle | Length x Width |
| Area of a Square | Side x Side |
| Area of a Rhombus | 1/2 x Diagonal 1 x Diagonal 2 OR Base x Height |
| Area of a Kite | 1/2 x Diagonal 1 x Diagonal 2 |
Problems on Quadrilaterals
Q.1: Find the area of the rectangle whose length is 4 cm and width is 3.5 cm.
Solution: Given, Length of the rectangle = 4 cm
And width of the rectangle = 3.5 cm
Since, area of the rectangle, A = Length x Width
A = 4 cm x 3.5 cm
A = 14 cm2
Q.2 If the area of the square is 121 cm2, then find the length of its sides.
Solution: Given, Area of the square = 121 cm2
We know,
Area of the square = side2
Therefore,
121 = side2
Or Side = √121 = 11
Hence, the side of the square is 11 cm.
Related Links
| Quadrilateral | Quadrilateral Angle Sum Property |
| Important Questions Class 8 Maths Chapter 3 Understanding Quadrilaterals | Quadrilaterals Class 9 |