In geometry, triangle is one of the basic shapes. Triangle is the smallest polygon. It consists of three edges and three vertices. A triangle with vertices P, Q and R is denoted as ∆PQR. In a triangle, three sides and three angles are referred to as the elements of the triangle. Angle sum property and exterior angle property are the two important attributes of a triangle. What is angle sum property of a triangle? How to prove angle sum property? It is discussed here on.

A triangle consists of interior and exterior angles. Interior angle is defined as the angle formed between two adjacent sides of a triangle. Exterior angle is defined as the angle formed between a side of triangle and an adjacent side extending outward.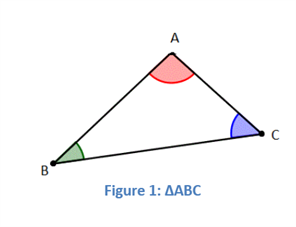For ∆ABC, Angle sum property of triangle declares that

Sum of all the interior angles of the triangle is 180°.

That is,

[latex]m\angle{A}~+~m\angle{B}~+~m\angle{C}[/latex] = [latex]180^{\circ}[/latex]

Proof of Angle Sum Property Theorem

These are the following steps involved to prove angle sum property theorem:

Step 1: Draw a line AB through the vertex P and parallel to the side QR of a triangle PQR.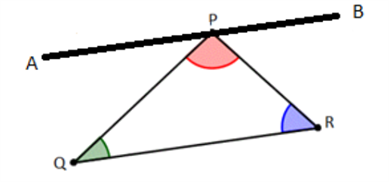

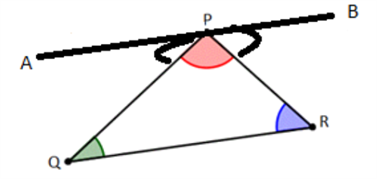
Step 2: Now, [latex]\angle{APQ}~+~\angle{QPR}~+~\angle{RPB}[/latex] = [latex]180^{\circ}[/latex][Linear Pair Axiom] —— (1)

Step 3:[latex]\angle{APQ}[/latex] = [latex]\angle{PQR}[/latex] [Alternate interior angles] —– (2)

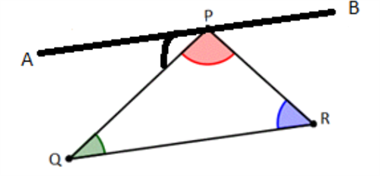
Step 4: [latex]\angle{RPB}[/latex] = [latex]\angle{PRQ}[/latex]  [Alternate interior angles] —– (3)

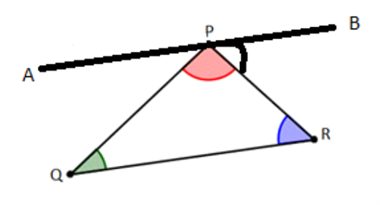
Step 5: Substituting [latex]∠APQ[/latex] and [latex]∠RPB[/latex] in equation 1 by [latex]∠PQR[/latex] and [latex]∠PRQ[/latex] respectively,

We have thus proved the angle sum property of a triangle. For the complete understanding of the topic please visit www.byjus.com or download the BYJU’S– The Learning App.