Area Of A Kite
Rhombus- A rhombus is a quadrilateral in which all the four sides are of equal length. Unlike a square, none of the interior angles of a rhombus is not \(90^{\circ}\) in measure.

Kite
A quadrilateral figure is having two pairs of equal adjacent sides, symmetrical only about one diagonal.
The diagonals of a kite are perpendicular.
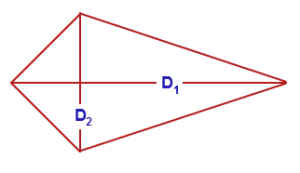
Area of a Kite
If we know the diagonals of a kite, it is possible to calculate the area of a kite.
Let \(D_{1}\) and \(D_{2}\) be the long and short diagonals of the kite, respectively.
Then the area of a kite is given by –
A = \(\frac{1}{2}D_{1}D_{2}\)
Proof for Area of a Kite
Let us consider a kite ABCD. Let diagonals AB(\(D_{1}\)) and CD(\(D_{2}) \) meet at point E. Thus we see that a diagonal divides a kite into two triangles.
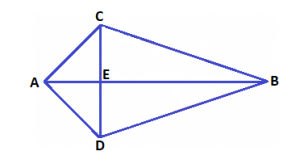
In the figure given above, we see that Diagonal AB divides a kite in two triangle ACB and ADB.
Thus area of traingles equal to –
\(Area (\bigtriangleup ACB) = \frac{1}{2} \times AB \times CE\)
and, \(Area (\bigtriangleup ADB) = \frac{1}{2} \times AB \times DE\)
Area of a Kite \( = Area (\bigtriangleup ACB) + Area (\bigtriangleup ADB)= \frac{1}{2} \times AB \times CE + \frac{1}{2} \times AB \times DE\)
Area of a Kite \( = \frac{1}{2} \times AB \times (CE + DE)\)
Area of a Kite \(= \frac{1}{2} \times AB \times (CD) = \frac{1}{2} \times D_{1} \times D_{2}\)
| Solved Example-
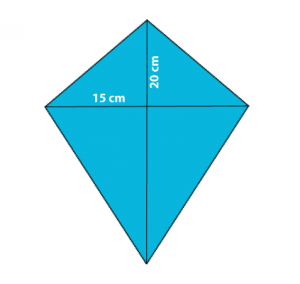
Example: Find the area of kite whose diagonals are 20 cm and 15 cm. Solution: We know, Area of a kite \( = \frac{1}{2}D_{1}D_{2}\) Area \( = \frac{1}{2} \times 20 \times 15 \;\;cm^{2}\) \(= 150 cm^{2}\)
|
If lengths of unequal sides are given, using Pythagoras theorem, the length of diagonals can be found.
| Example: The sides of a kite are given as follows
Find the area of a kite. Solution: Given IK = \(8\sqrt{2}\)KE = 17 Construction- Draw in segment KT and segment IE as shown in the figure alongside
In Triangle IKX, it is clear that \(\angle XKI = XIK\) So, the length KX = XI Using Pythagoras Theorem, we have \(KX^{2}+XI^{2}= KI^{2}\) \(XI^{2}+XI^{2}= KI^{2}\) \(2 XI^{2}= \left ( 8\sqrt{2} \right )^{2}\) Therefore \(XI = KX = 8\) units In Triangle KEX, using Pythagoras theorem we have \(KX^{2}+XE^{2}= KE^{2}\) \(8^{2} + XE^{2} = 17^{2}\) \(XE^{2} = 289 – 64 = 225 \) Therefore \(XE = 15\) units Thus the length of diagonals are – Diagonal KT = KX + XT = 8 + 8 = 16 units Diagonal IE = IX + XE = 8 + 15 = 23 units Area = \(\frac{1}{2} \times D_{1} \times D_{2}\) \(= \frac{1}{2} \times 16 \times 23 \;\; unit^{2}\) = \(184 \; units^{2}\) |
This was all about kite. Learn various related concepts of topics like Quadrilateral, Trapezoid, Rhombus, Rectangle, Square, etc. in an engaging manner by visiting our site BYJU’S.
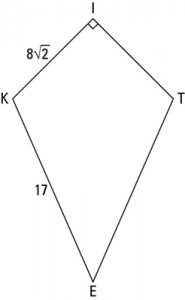
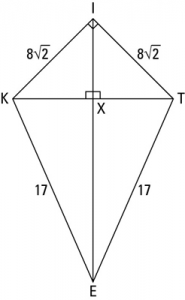 To find the area of a kite, first, we need to calculate the length of the diagonals KT, EI.
To find the area of a kite, first, we need to calculate the length of the diagonals KT, EI.