Collinear points are the points that lie on the same straight line or in a single line. If two or more than two points lie on a line close to or far from each other, then they are said to be collinear, in Euclidean geometry.

Collinear Points Definition

The term collinear is the combined word of two Latin names ‘col’ + ‘linear’. ‘Col’ means together and ‘Linear; means line. Therefore, collinear points mean points together in a single line. You may see many real-life examples of collinearity such as a group of students standing in a straight line, a bunch of apples kept in a row, next to each other, etc.

In geometry, two or more points are said to be collinear, if they lie on the same line. Hence the collinear points are the set of points that lie on a single straight line.

What are Collinear points in Maths?

From the above definition, it is clear that the points which lie on the same line are collinear points. To understand this concept clearly, consider the below figure and try to categorize the collinear and non-collinear points.

In the above figure, the set of collinear points are {A, D}, {A, C, F}, {A, P, R}, {Q, E, R} and {F, B, R}. The remaining points are said to be non-collinear, i.e. {P, B}, {C, E} and so on.

Collinear Meaning

If we say, that three objects are placed in a line, that means the objects are collinear.

In more astonishing observation, the term collinear has been used for straightened things, that means, something being “in a row” or “in a line”.

Non-Collinear Points

The set of points that do not lie on the same line are called non-collinear points. We cannot draw a single straight line through these points. The example of non-collinear points is given below:

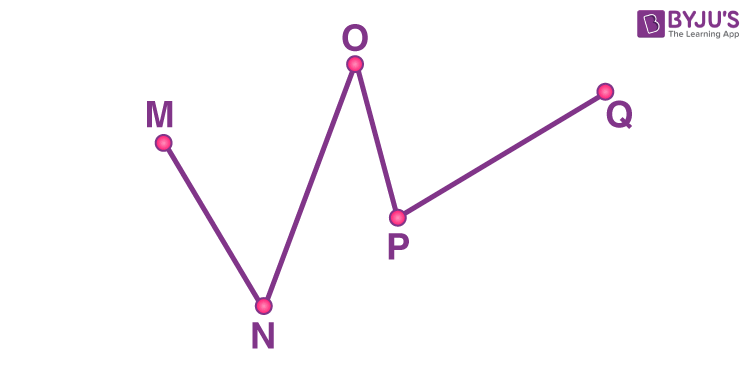
Collinear Points Formula

There are three methods to find the collinear points. They are:

• Distance Formula
• Slope Formula
• Area of triangle

Using Distance Formula

If P, Q and R are three collinear points, then,

Distance from P to Q + Distance from Q to R = Distance from P to R

PQ + QR = PR

Now, by the distance formula we know, the distance between two points (x1, y1) and (x2, y2) is given by;

\(D=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)

Hence, we can easily find the distance between the points P, Q and R, with the help of this formula. 

Using Slope Formula

Three or more points are said to be collinear if the slope of any two pairs of points is the same. The slope of the line basically measures the steepness of the line.

Suppose, X, Y and Z are the three points, with which we can form three sets of pairs, such that, XY, YZ and XZ are three pairs of points. Then, as per the slope formula,

If Slope of XY = Slope of YZ = Slope of XZ, then the points X, Y and Z are collinear.

Note: Slope of the line segment joining two points say (x₁, y₁) and (x₂, y₂) is given by the formula:

m = (y₂ – y₁)/ (x₂ – x₁)

Using the Area of Triangle Formula

If the area of triangle formed by three points is zero, then they are said to be collinear. It means that if three points are collinear, then they cannot form a triangle.

Suppose, the three points P(x₁, y₁), Q(x₂, y₂) and R(x₃, y₃) are collinear, then by remembering the formula of area of triangle formed by three points we get;

\(\frac{1}{2}\begin{vmatrix} x_{1}-x_{2} & x_{2}-x_{3} \\ y_{1}-y_{2} & y_{2}-y_{3} \end{vmatrix}=0\)

Or

(1/2) | [x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃[y₁ – y₂]| = 0

Related Articles

• Coordinate System
• Coordinates of A Point in Three Dimensions
• Distance Between Two Points
• Equation Of A Plane: 3 Non-Collinear Points

Solved Examples

Example 1: Find if the points P(−3,−1), Q(−1,0), and R(1,1) are collinear.

Solution: The points P, Q and R are collinear, if;

(Distance between P and Q) + (Distance between Q and R) = Distance between P and R

By Distance formula, we can find the distance between two points.

So,

\(\begin{aligned} \text { Distance between } \mathrm{PQ} &=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}} \\ &=\sqrt{(-1+3)^{2}+(0+1)^{2}} \\ &=\sqrt{5} \end{aligned}\)

\(\begin{aligned} \text { Distance between Q and R } &=\sqrt{\left(x_{3}-x_{2}\right)^{2}+\left(y_{3}-y_{2}\right)^{2}} \\ &=\sqrt{(1+1)^{2}+(1-0)^{2}} \\ &=\sqrt{5} \end{aligned}\)

\(\begin{aligned} \text { Distance between P and R } \mathrm{AC} &=\sqrt{\left(x_{3}-x_{1}\right)^{2}+\left(y_{3}-y_{1}\right)^{2}} \\ &=\sqrt{(1+3)^{2}+(1+1)^{2}} \\ &=\sqrt{20}\\ &=2 \sqrt{5} \end{aligned}\)

Hence we can conclude that,

√5 + √5 = 2√5

PQ + QR = PR

Therefore, P, Q and R are collinear.

Example 2: Show that the three points P(2, 4), Q(4, 6) and R(6, 8) are collinear.

Solution: If the three points P(2, 4), Q(4, 6) and R(6, 8) are collinear, then slopes of any two pairs of points, PQ, QR & PR will be equal.

Now, using slope formula we can find the slopes of the respective pairs of points, such that;

Slope of PQ = (6 – 4)/ (4 – 2) = 2/2 = 1

Slope of QR = (8 – 6)/ (6 – 4) = 2/2 = 1

Slope of PR = (8 – 4) /(6 – 2) = 4/4 = 1

As we can see, the slopes of all the pairs of points are equal.

Therefore, the three points P, Q and R are collinear.

Example 3: Find if P(2, 3), Q(4, 0) and R(6, -3) are collinear points.

Solution: As per the area of triangle formula for three coordinates in a plane,

Area = \(\frac{1}{2}\begin{vmatrix} 2-4 & 4-6 \\ 3-0 & 0+3 \end{vmatrix}\\ = \frac{1}{2}\begin{vmatrix} -2 & -2\\ 3 & 3 \end{vmatrix}\)

Area = ½ (6 – 6)

Area = 0

Hence, the points P, Q and R are collinear.

Practice Questions

• Check whether the given points P (3,7), Q (6,5) and R (15,-1) are collinear.
• Check if the given points P(0,3), Q (1,5) and C (-1,1) are collinear.
• If A (5,2), B (3,-2) and C (8,8) are three points in a plane. Check whether the points are collinear.
• Show that the points A(1,-1) B(6,4) and C(4,2) are collinear, using the distance formula.
• Prove that the points A(7, -5), B(9, -3) and C( 13 1)  are collinear, using section formula.

For more maths articles, visit byjus.com and download BYJU’S – The Learning App for exciting learning videos.