In mathematics, commutative property or commutative law explains that order of terms doesn’t matter while performing arithmetic operations. 

Commutative property is applicable only for addition and multiplication processes. Thus, it means we can change the position or swap the numbers when adding or multiplying any two numbers. This is one of the major properties of integers.

For example: 1+2 = 2+1 and 2 x 3 = 3 x 2. 

What is Commutative Property?

As we already discussed in the introduction, as per the commutative property or commutative law, when two numbers are added or multiplied together, then a change in their positions does not change the result. 

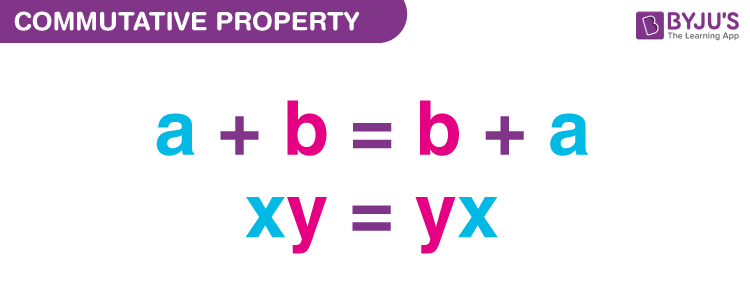
Examples

• 2+3 = 3+2 = 5
• 2 x 3 = 3 x 2 = 6
• 5 + 10 = 10 + 5 = 15
• 5 x 10 = 10 x 5 = 50

So, there can be two categories of operations that obeys commutative property:

• Commutative property of addition
• Commutative property of multiplication

History

Although the official use of commutative property began at the end of the 18th century, it was known even in the ancient era.

The word, Commutative, originated from the French word ‘commute or commuter’ means to switch or move around, combined with the suffix ‘-ative’ means ‘tend to’. Therefore, the literal meaning of the word is tending to switch or move around. It states that if we swipe the positions of the integers, the result will remain the same.

Commutative Property of Addition

According to the commutative property of addition, when we add two integers, the answer will remain unchanged even if the position of the numbers are changed.

Let A and B be the two integers, then;

Examples of Commutative Property of Addition

• 1 + 2 = 2 + 1 = 3
• 3 + 8 = 8 + 3 = 11
• 12 + 5 = 5 + 12 = 17

Commutative Property of Multiplication

As per the commutative property of multiplication, when we multiply two integers, the answer we get after multiplication will remain the same, even if the position of the integers are interchanged.

Let A and B be the two integers, then;

Examples of Commutative Property of Multiplication

• 1 × 2 = 2 × 1 = 2
• 3 × 8 = 8 × 3 = 24
• 12 × 5 = 5 × 12 = 60

Important Facts Of Commutative Property

• Commutative property is only applicable for two arithmetic operations: Addition and Multiplication
• Changing the order of operands, does not change the result 
• Commutative property of addition: A + B = B + A
• Commutative property of multiplication: A.B = B.A

Other Properties

The other major properties of addition and multiplication are:

• Associative Property
• Distributive Property

Now, observe the other properties as well here:

Associative Property of Addition and Multiplication

According to the associative law, regardless of how the numbers are grouped, you can add or multiply them together, the answer will be the same. In other words, the placement of parentheses does not matter when it comes to adding or multiplying.

Hence,

Examples: 

• 1 + (2+3) = (1+2) + 3 → 6
• 3 x (4 x 2) = (3 x 4) x 2 → 24

Distributive Property of Multiplication

The distributive property of Multiplication states that multiplying a sum by a number is the same as multiplying each addend by the value and adding the products then.

According to the Distributive Property, if a, b, c are real numbers, then:

a x (b + c) = (a x b) + (a x c)

Example:

• 2 x (5 x 8) = (2 x 5) + (2 x 8) → 80

There are certain other properties such as Identity property, closure property which are introduced for integers.

Non-Commutative Property

Some operations are non-commutative. By non-commutative, we mean the switching of the order will give different results. The mathematical operations, subtraction and division are the two non-commutative operations. Unlike addition, in subtraction switching of orders of terms results in different answers.

Example: 4 – 3 = 1 but 3 – 4 = -1 which are two different integers.

Also, the division does not follow the commutative law. That is,

6 ÷ 2 = 3

2 ÷ 6 = 1/3

Hence, 6 ÷ 2 ≠  2 ÷ 6

Solved Examples on Commutative Property

Example 1: Which of the following obeys commutative law?

1. 3 ×  12
2. 4 + 20
3. 36 ÷ 6
4. 36 – 6
5. -3 × 4

Solution: Options 1, 2 and 5 follow the commutative law

Explanation:

1. 3 × 12 = 36 and

       12 x 3 = 36

=> 3 x 12 = 12 x 3 (commutative)

2. 4 + 20 = 24 and

     20 + 4 = 24

     => 4 + 20 = 20 + 4 (commutative)

3. 36 ÷ 6 = 6 and

     6 ÷ 36 = 0.167

=> 36 ÷ 6 ≠ 6 ÷ 36  (non commutative)

4. 36 − 6 = 30 and 

      6 – 36 = – 30

=> 36 – 6 ≠ 6 – 36  (non commutative)

5. −3 × 4 = -12 and

       4 x -3 = -12

=> −3 × 4 = 4 x -3  (commutative)

Q.2: Prove that a+ b = b+a if a = 10 and b = 9.

Sol: Given that, a = 10 and b = 9 

LHS = a+b = 10 + 9 = 19   ……(1)

RHS = b + a = 9 + 10 = 19 ……(2)

By equation 1 and 2, as per commutative property of addition, we get;

LHS = RHS

Hence, proved.

Q.3: Prove that A.B = B.A, if A = 4 and B = 3.

Sol: Given, A = 4 and B = 3.

A.B = 4.3 = 12  ….. (1)

B.A = 3.4 = 12  …..(2)

By eq.(1) and (2), as per the commutative property of multiplication, we get;

LHS = RHS

A.B = B.A

Hence, proved.

Practice Questions

Find which of the following is the commutative property of addition and multiplication.

• 3 + 4 = 4 + 3
• 10 x 7 = 7 x 10
• 8 x 9 = 9 x 8
• 6 + 4 = 4 + 6

To solve more problems on properties of math, download BYJU’S – The Learning App from Google Play Store and watch interactive videos.