We know that there are infinite points in the coordinate plane. Consider an arbitrary point P(x,y) on the XY plane and a line L. How will we confirm whether the point is lying on the line L? This is where the importance of equation of a straight line comes into the picture in two-dimensional geometry.

Equation of a straight line contains terms in x and y. If the point P(x,y) satisfies the equation of the line, then the point P lies on the line L.

Different forms of equations of a straight line

1. Equations of horizontal and vertical lines

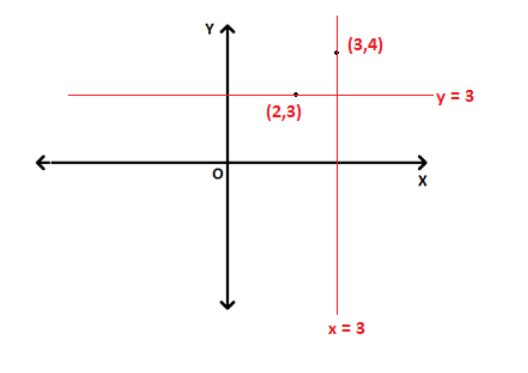
Equation of the lines which are horizontal or parallel to the X-axis is y = a, where a is the y – coordinate of the points on the line.

Similarly, equation of a straight line which is vertical or parallel to Y-axis is x = a, where a is the x-coordinate of the points on the line.

For example, the equation of the line which is parallel to X-axis and contains the point (2,3) is y= 3.

Similarly, the equation of the line which is parallel to Y-axis and contains the point (3,4) is x = 3.

2. Point-slope form equation of line

Consider a non-vertical line L whose slope is m, A(x,y) be an arbitrary point on the line and \(P(x_1,y_1)\) be the fixed point on the same line.

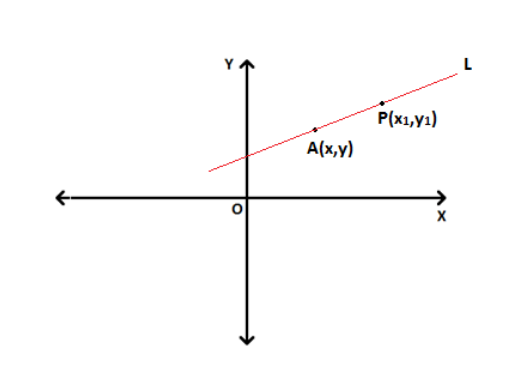
Slope of the line by the definition is,

\(m\) = \(\frac{y~-~y_1}{x~-~x_1}\)

\(y~-~y_1\) = \(m(x~-~x_1)\)

For example, equation of the straight line having a slope \(m\) = \(2\) and passes through the point \((2,3)\) is

y – 3 = 2(x – 2)

y= 2x-4+3

2x-y-1 = 0

3. Two-point form equation of line

Let P(x,y) be the general point on the line L which passes through the points \(A(x_1,y_1)\) and \(B(x_2,y_2)\).

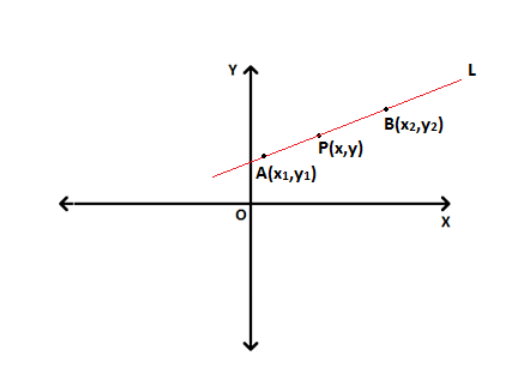
Since the three points are collinear,

slope of PA = slope of AB

\(\frac{y~-~y_1}{x~-~x_1}\) = \(\frac{y_2~-~y_1}{x_2~-~x_1}\)
\(y – y_{1} = (y_{2} – y_{1}). \frac{x – x_{1} }{x_{2} – x_{1}}\)

4. Slope-intercept form equation of line

Consider a line whose slope is \(m\) which cuts the \(Y\)-axis at a distance ‘a’ from the origin. Then the distance a is called the \(y\)– intercept of the line. The point at which the line cuts \(y\)-axis will be \((0,a)\).

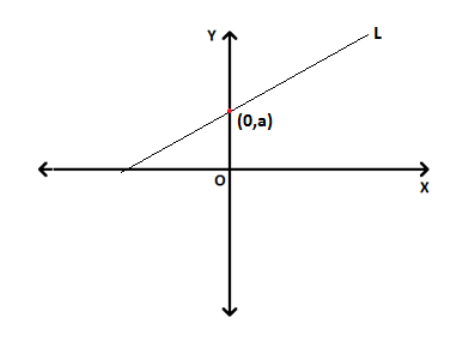
Then, equation of the line will be

y-a = m(x-0)

y = mx+a

Similarly, a straight line having slope m cuts the X-axis at a distance b from the origin will be at the point (b,0). The distance b is called x- intercept of the line.

Equation of the line will be:

y = m(x-b)

5. Intercept form

Consider a line L having x– intercept a and y– intercept b, then the line touches X– axis at (a,0) and Y– axis at (0,b).

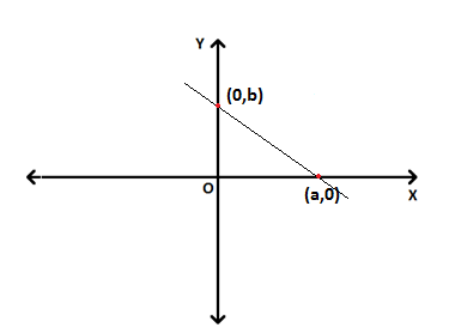
By two-point form equation,

\(y~-~0\) = \(\frac{b-0}{0~-~a} (x~-~a)\)

\(y\) = \(-\frac{b}{a} (x~-~a)\)

\(y\) = \(\frac{b}{a} (a~-~x)\)

\(\frac{x}{a} ~+ ~\frac{y}{b} \) = \(1\)

For example, equation of the line which has \(x\)– intercept \(3\) and \(y\)– intercept \(4\) is,

\(\frac{x}{3} ~+ ~\frac{y}{4}\) = \(1\)

\(4x~ + ~3y\) = \(12\)

6. Normal form

Consider a perpendicular from the origin having length l to line L and it makes an angle β with the positive X-axis.

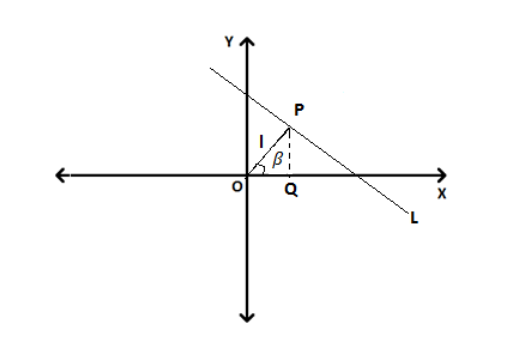
Let OP be the perpendicular from the origin to the line L.
Then,

\(OQ\) = \(l~ cosβ\)

\(PQ\) = \(l~ sinβ\)

Coordinates of the point \(P\) are; \(P(l ~cos~β,l ~sin~β)\)

slope of the line \(OP\) is \(tan~β\)

Therefore,

\(Slope~ of ~the ~line ~L\) = \(-\frac{1}{tan~β}\) = \(-\frac{cos~β}{sin~β}\)

Equation of the line \(L\) having slope \(-\frac{cos~β}{sin~β}\) and passing through the point \((l ~cos~β,l ~sin~β)\) is,

\(y~-~l~ sin~β\) = \(-\frac{cos~β}{sin~β} (x~-~l ~cosβ)\)

\(y ~sin~β~-~l~ sin^2~ β\) = \(-x ~cos~β~+~l~cos^2~β\)

\(x~ cos~β~ + ~y ~sin~β\) = \(l(sin^2~β ~+ ~cos^2~β)\)

\(x ~cos~β~ + ~y ~sin~β\) = \(l\)

You have learnt about the different forms of equation of a straight line. To know more about straight lines and its properties, log onto www.byjus.com.’