Factors Of 63
Factors of 63 are the integers that divide the original number evenly. There are totally six factors of 63, i.e., 1, 3, 7, 9, 21, and 63. Hence, the smallest factor is 1 and the greatest factor of 63 is 63, itself. Pair factors of 63 are the numbers which when multiplied in pairs results in the original number. The factors in Pairs are (1, 63), (3, 21), and (7, 9). If we add all the factors of 63, then the sum will be equal to: 1 + 3 + 7 + 9 + 21 + 63 = 104.
In this article, we will learn in detail how to find the factors of 63 using the division method and prime factorisation method. Also, see some examples related to factors of 63.
What are the Factors of 63?
The factors of 63 are the numbers that divide the number 63 exactly without leaving any remainder. In other words, the pair factors of 63 are the numbers that are multiplied in pairs resulting in the original number 63. Since the number 63 is a composite number, 63 has more than two factors. Thus, the factors of 63 are 1, 3, 7, 9, 21 and 63.

Pair Factors of 63
The pair factors of 63 are the numbers that are multiplied in pairs to give the product value as 63. As the factors of 63 can be positive or negative, the pair factors of 63 can also be positive or negative, but they cannot be in fraction or decimal form. Thus, the positive and negative pair factors of 63 are given below.
Positive Pair Factors of 63:
|
Positive Factors of 63 |
Positive Pair Factors of 63 |
|
1 × 63 |
(1, 63) |
|
3 × 21 |
(3, 21) |
|
7 × 9 |
(7, 9) |
Negative Pair Factors of 63:
|
Negative Factors of 63 |
Negative Pair Factors of 63 |
|
-1 ×- 63 |
(-1, -63) |
|
-3 × -21 |
(-3, -21) |
|
-7 × -9 |
(-7, -9) |
How to Find Factors of 63?
63 is an odd number that has six factors. Since the number of factors is less, thus it is easy to get these factors using two simple methods. They are:
- Division Method
- Prime Factorisation Method
Factors of 63 Using Division Method
Using a simple division method, we can evaluate the factors of 63. Let us start.
- Divide 63 with the smallest possible divisor, i.e.,1. Hence, one of the factors of 63 is 1.
- Now check with the next whole number, that can divide 63 completely. 63/3 = 21. Hence, 3 is a factor.
- Continue the division by whole number until we reach 63/63 = 1. Since, we cannot take the further whole numbers.
- Thus, the factors we have received are:
- 63/1 = 63
- 63/3 = 21
- 63/7 = 9
- 63/9 = 7
- 63/21 = 3
- 63/63 = 1
Hence, the required factors of 63 are 1,3,7,9,21 and 63.
Using Trick
Another trick to find the factors of 63 using division method is given below:
- Dividing 63 by 1 we get 63. (1 and 63 are the factors)
- Dividing 63 by 3 we get 21. (3 and 21 are the factors)
- Now we know 21 is also a composite number.
- Divide 21 by 3, we get 7 (Again 7 and 3 are the factors)
Hence, by the above steps, the numbers 1, 63, 21, 7 and 3 become the factors of 63. Since 3 is repeated twice, thus 3 x 3 = 9 is also a factor of 63. Therefore, the total factors are 1, 3, 7, 9, 21 and 63.
Prime Factorization of 63
The number 63 is a composite number. Now let us find the prime factors associated with 63.
- The first step is to divide the number 63 with the smallest prime factor,i.e. 2.
63 ÷ 2 = 31.5; fraction cannot be a factor. Therefore, moving to the next prime number
Divide 63 by 3.
63 ÷ 3 = 21
- Again divide 21 by 3 and keep on diving the output by 3 till you get 1 or a fraction.
21 ÷ 3 = 7
7 ÷ 3 = 2.33; cannot be a factor. Now move to the next prime number 7.
- Dividing 7 by 7 we get,
7 ÷ 7 = 1
- We have received 1 at the end and it doesn’t have any factor. Therefore, we cannot proceed further with the division method. So, the prime factorisation of 63 is 3 × 3 × 7 or 32 × 7, where 3 and 7 are the prime numbers.
Factor Tree of 63
By prime factorisation, we have seen, how we can split the number 63 into prime factors. Thus the factor tree so formed is shown in the figure below.
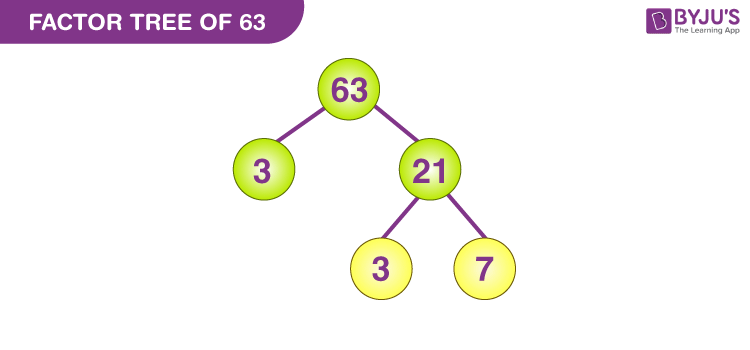
Facts of Factors of 63
- Factors of 63 – 1, 3, 7, 9, 21 and 63
- Prime factorisation of 63 – 3 × 3 × 7
- Prime factor of 63 – 3 and 7
- Pair factors of 63 – (1, 63), (3, 21), and (7, 9)
- Sum of factors of 63 – 104
Related Articles
| Links Related to Factors | |
| Factors of 15 | Factor of 36 |
| Factors of 48 | Factors of 18 |
| Factors of 42 | Factors of 60 |
| Factors of 35 | Factors of 27 |
| Factors And Multiples | Factors of 50 |
Solved Examples on Factors of 63
Example 1:
Find the common factors of 63 and 62.
Solution:
The factors of 63 are 1, 3, 7, 9, 21 and 63
The factors of 62 are 1, 2, 31, 62.
Thus, the common factor of 63 and 62 is 1.
Example 2:
Find the common factors of 63 and 64.
Solution:
Factors of 63 = 1, 3, 7, 9, 21 and 63
Factors of 64 = 1, 2, 4, 8, 16, 32 and 64
Therefore, the common factors of 63 and 64 is 1.
Example 3:
Find the common factors of 63 and 61.
Solution:
The factors of 63 are 1, 3, 7, 9, 21 and 63
The factors of 61 are 1 and 61.
Hence, the common factor of 63 and 61 is 1 only, as 61 is a prime number.
Practise Questions on Factors of 63
- What are the common factors of 63 and 65?
- Which is the second highest factor of 63?
- What is the difference between highest factor and smallest factor of 63?
- What is the greatest common factor of 63 and 70?
Learn more about factors and prime factors here with us in BYJU’S and also download BYJU’S – The Learning App for a better experience and get video content to study and understand the concepts of Maths topics.
Frequently Asked Questions on Factors of 63
What are the factors of 63?
The factors of 63 are the numbers that divide 63, without leaving any remainder. Hence, the factors of 63 are 1, 3, 7, 9, 21 and 63.
What is the prime factorization of 63?
The prime factorization of 63 is 3 × 3 × 7 or 32 × 7.
Write down the positive pair factors of 63?
The positive pair factors of 63 are (1, 63), (3, 21), and (7, 9).
What are the negative pair factors of 63?
The negative pair factors of 63 are (-1, -63), (-3, -21) and (-7, -9).
Is 21 a factor of 63?
Yes, 21 is a factor of 63. As the number 21 divides 63 exactly, 21 is a factor of 63.