Square root of a number is the value that returns the original number on multiplied by itself. Finding square root by prime factorisation is an easy method. We need to factories the number under the root and pair them in two. For example, the square root of 9 is √9 = √(3×3) = 3.

We can see, 9 is a perfect square and hence it is easier to find the root of such numbers. For imperfect squares, we can use long division method to find the square root.

How to Find Square Root By Prime Factorisation?

The inverse process of subtraction is addition and of division is multiplication. In the same way, the inverse of squaring a number is finding its root. For instance,

1² = 1, the square root of 1 is 1

4² = 16, square root of 16 is 4 and so on

Prime Factorisation

Let us consider the prime factors of a number and its square. For example 12 and 144,

12 = 2 × 2 × 3

144 = 2 × 2 × 3 × 2 × 2 × 3

It can be observed that the prime factors in the prime factorisation of a square number, occur twice the number of times, it occurs in the number itself. For example, let us find the prime factors of 576.

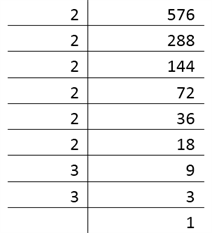
For finding the square root, firstly we have to pair the common factors.

\(576\) = \(\underline{2~ ×~ 2} ~×~\underline{ 2 ~×~ 2} ~×~ \underline{2~ ×~ 2} ~×~\underline{ 3~ ×~ 3}\)

\(\Rightarrow~ 576\) = \(2^2~ × ~2^2 ~× ~2^2~ ×~ 3^2\)

The square root of 576 will be:

\(2 ~× ~2 ~×~ 2~ ×~ 3\) = \(24\)

Solved Examples

Let us see here some more examples to find square root of numbers.

Q.1: Find the square root of 8.

Solution: We can write, 8 as:

8 = 2 x 2 x 2

Hence,

√8 = √(2 x 2 x 2) = 2√2

Q.2: Find the root of 81.

Solution: We can write 81 as:

81 = 3 x 3 x 3 x 3

√81 = √(3 x 3 x 3 x 3)

√81 = 3 x 3 = 9

Q.3: What is the root of 324?

Solution: The prime factorisation of 324 can be written as:

324 = 2  x 2 x 3 x 3 x 3 x 3

√324 = √(2  x 2 x 3 x 3 x 3 x 3)

√324 = 2 x 3 x 3 = 18

Practice Questions

Find the square root of numbers using prime factorisation method.

1. 400
2. 1024
3. 2025
4. 4096

Application of square root

Area of a square is the product of its sides. In a square, all the sides have the same length. Hence, if one of the sides is known then the area can be easily calculated. Area of square = Side × Side = Side².

Now, what if the area of the square is given, and we have to calculate the length of its side? This can easily be done by finding the square root of the area. The value obtained after calculating the square root will be the length of its side.

For example, the area of a square is 225. Its length will be:

225 = a²

⇒ 15 × 15 = a²

⇒a = 15

Therefore, the side of the square is 15 units.

This article covers the method of prime factorisation. To learn more about other topics download BYJU’S – The Learning App and watch interactive videos. Also, take free tests to practice for exams.

Video Lesson