You may have already learnt about the properties and types of triangles. One of the special types of a triangle is the isosceles triangle. An isosceles triangle is a triangle which has two equal sides, no matter in what direction the apex (or peak) of the triangle points. Some pointers about isosceles triangles are:

• It has two equal sides.
• It has two equal angles, that is, the base angles.
• When the third angle is 90 degree, it is called a right isosceles triangle.

In this article, we have given two theorems regarding the properties of isosceles triangles along with their proofs.

Isosceles Triangle Theorems and Proofs

Theorem 1: Angles opposite to the equal sides of an isosceles triangle are also equal.

Proof: Consider an isosceles triangle ABC where AC = BC.

We need to prove that the angles opposite to the sides AC and BC are equal, that is, ∠CAB = ∠CBA.

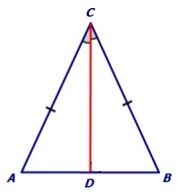
We first draw a bisector of ∠ACB and name it as CD.

Now in ∆ACD and ∆BCD we have,

AC = BC                                                                (Given)

∠ACD = ∠BCD                                                    (By construction)

CD = CD                                                               (Common to both)

Thus,  ∆ACD ≅∆BCD                                        (By SAS congruence criterion)

So, ∠CAB = ∠CBA                                              (By CPCT)

Hence proved.

Theorem 2: Sides opposite to the equal angles of a triangle are equal.

Proof: In a triangle ABC, base angles are equal and we need to prove that AC = BC or ∆ABC is an isosceles triangle.

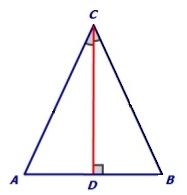
Construct a bisector CD which meets the side AB at right angles.

Now in ∆ACD and ∆BCD we have,

∠ACD = ∠BCD                                                    (By construction)

CD = CD                                                               (Common side)

∠ADC = ∠BDC = 90°                                          (By construction)

Thus, ∆ACD ≅ ∆BCD                                         (By ASA congruence criterion)

So, AC = BC                                                         (By CPCT)

Or ∆ABC is isosceles.

To learn more about isosceles triangles, their properties and examples based on the theorems discussed above, download BYJU’S – The Learning App.