Limits and Derivatives Class 11
Limits and Derivatives Class 11 Notes
Limits and derivatives class 11 notes cover concepts such as the intuitive idea of derivatives, limits, and trigonometry functions and derivatives. Limits and derivatives have the scope, not only in Maths but also they are highly used in Physics to derive some particular derivations. We will discuss here the Class 11 limits and derivatives syllabus with properties and formulas.
Class 11 Chapter 13 Limits and Derivatives Concepts
The limits and derivatives chapter of class 11 includes the following concepts.
- Introduction
- Intuitive Idea of Derivatives
- Limits
- Limits of Trigonometric Functions
- Derivatives
Let us learn and understand all the concepts in limits and derivatives.
| Read more: |
Limits Definition
A limit of a function f(x) is defined as a value, where the function reaches as the limit reaches some value. Limits are used to define integration, integral calculus and continuity of the function.
If f(y) is a function, then the limit of the function can be represented as;
limy→c
This is the general expression of limit, where c is any constant value. But there are some important properties of limits which we will discuss here.
Also, check: Sandwich theorem
Properties of limits of a given function
A. Let ‘p’ and ‘q’ be any two functions and ‘a’ be any constant value in such a way that, there exists, limx→a p(x) and limx→a q(x). Now, check below the properties of limits.
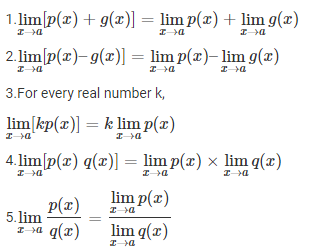
B. For any positive integers m,
limx→a p(x)(xm-am )/(x-a)= nam-1
Also, learn about the algebra of limits here.
C. Limits of trigonometric functions:
If p and q are real-valued functions with the same domain, such that, p(x) ≤ q(x) for all the values of x. For a value b, if both limx→a p(x) and limx→a q(x) exists then,
limx→a p(x) ≤ limx→a q(x)
To understand more about the limits of trigonometric functions, visit here.
Example:Let f(x) = x2 – 4. Compute \(\lim_{ x \rightarrow 2} f(x)\).
Solution: \(\lim_{ x \rightarrow 2} f(x)\) = \(\lim_{ x \rightarrow 2} x^2 – 4\)
= 22 – 4 = 4 – 4 = 0
To know the limits of polynomials and rational functions, visit here.
Derivatives Definition
A derivative is defined as the rate of change of a function or quantity with respect to others. The formula for derivative can be represented in the form of;
\(\lim_{ a \rightarrow 0} \frac{f(x+a)- f(x)}{a}\)The derivative of a function f(x) is denoted as f’(x). Now, let us see the properties of derivatives.
Properties of derivatives for given functions:
Let for functions p(x) and q(x), the properties of derivatives are;
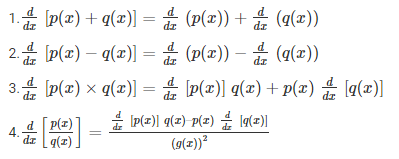
Also, read: Derivatives of polynomials and trigonometric functions
Let’s have a look at the example given below:
Example: Calculate d/dx(x4+1)
Solution:
We know,
d/dx(xn)= n xn-1 and the derivative of a constant value is 0.
Therefore,
d/dx(x4+1)= 4x3
General Derivative Formulas
| Derivative of a function | Result |
| \(\frac{d(x)}{dx}\) | 1 |
| \(\frac{d(ax)}{dx}\) | a |
| \(\frac{d(x^n)}{dx}\) | nxn-1 |
| \(\frac{d(sin\ x)}{dx}\) | cos x |
| \(\frac{d(cos\ x)}{dx}\) | -sin x |
| \(\frac{d(tan\ x)}{dx}\) | sec2x |
| \(\frac{d(cosec\ x)}{dx}\) | -cosec x cot x |
| \(\frac{d(sec\ x)}{dx}\) | sec x tan x |
| \(\frac{d(cot\ x)}{dx}\) | -cosec2x |
| \(\frac{d(ln x)}{dx}\) | 1/x |
| \(\frac{d(e^x)}{dx}\) | ex |
| \(\frac{d(a^x)}{dx}\) | ax (log a) |
Get more differentiation formulas here.
Limits and Derivatives of Class 11 Important Questions and Solutions
Question 1:
Evaluate: limx→2[(x2-4)/(x-2)]
Solution:
limx→2[(x2-4)/(x-2)] = limx→2[(x+2)(x-2)/(x-2)]
Cancel the term x-2 from numerator and denominator. Now we get,
limx→2 x+2 = 2+2 = 4
Question 2:
Solve limx→2 (sin 2x/x)
Solution:
Given, limx→2 (sin 2x/x)
We can write it as;
limx→2 (sin 2x/2x) × 2
Since, limx→2 (sin x/x)= 1
Therefore, limx→2 (sin 2x/2x) × 2 = 1 × 2 = 2
Practice Problems
- Find the derivative of f(x) = sin x + cos x using the first principle.
- Evaluate: limx→4 (4x + 3)/(x – 2)
- Find the derivative of the function f(x) = 2x2 + 3x – 5 at x = –1. Also prove that f′(0) + 3f′(–1) = 0
Get more important questions class 11 Maths Chapter 13 limit and derivatives here with us and practice yourself.
Download BYJU’S app and learn Maths topics relevant to your class with interactive videos.