Linear Equations
Linear equations are equations of the first order. The linear equations are defined for lines in the coordinate system. When the equation has a homogeneous variable of degree 1 (i.e. only one variable), then it is known as a linear equation in one variable. A linear equation can have more than one variable. If the linear equation has two variables, then it is called linear equations in two variables and so on. Some of the examples of linear equations are 2x – 3 = 0, 2y = 8, m + 1 = 0, x/2 = 3, x + y = 2, 3x – y + z = 3. In this article, we are going to discuss the definition of linear equations, standard form for linear equation in one variable, two variables, three variables and their examples with complete explanation.
Table of Contents:
- Definition
- Forms of Linear Equation
- How to Solve Linear Equations
- Solving Linear Equations
- Practice Questions
- FAQs
Linear Equation Definition
An equation is a mathematical statement, which has an equal sign (=) between the algebraic expression. Linear equations are the equations of degree 1. It is the equation for the straight line. The solutions of linear equations will generate values, which when substituted for the unknown values, make the equation true. In the case of one variable, there is only one solution. For example, the equation x + 2 = 0 has only one solution as x = -2. But in the case of the two-variable linear equation, the solutions are calculated as the Cartesian coordinates of a point of the Euclidean plane.
Below are some examples of linear equations in one variable, two variables and three variables:
| Linear Equation in One variable | Linear Equation in Two variables | Linear Equation in Three variables |
|
3x+5=0 (3/2)x +7 = 0 98x = 49 |
y+7x=3 3a+2b = 5 6x+9y-12=0 |
x + y + z = 0 a – 3b = c 3x + 12 y = ½ z |
Forms of Linear Equation
The three forms of linear equations are
- Standard Form
- Slope Intercept Form
- Point Slope Form
Now, let us discuss these three major forms of linear equations in detail.
Standard Form of Linear Equation
Linear equations are a combination of constants and variables. The standard form of a linear equation in one variable is represented as
| ax + b = 0, where, a ≠ 0 and x is the variable. |
The standard form of a linear equation in two variables is represented as
| ax + by + c = 0, where, a ≠ 0, b ≠ 0 , x and y are the variables. |
The standard form of a linear equation in three variables is represented as
| ax + by + cz + d = 0, where a ≠ 0, b ≠ 0, c ≠ 0, x, y, z are the variables. |
Slope Intercept Form
The most common form of linear equations is in slope-intercept form, which is represented as;
y = mx + b
Where,
m is the slope of the line,
b is the y-intercept
x and y are the coordinates of the x-axis and y-axis, respectively.
For example, y = 3x + 7:
slope, m = 3 and intercept = 7
If a straight line is parallel to the x-axis, then the x-coordinate will be equal to zero. Therefore,
y=b
If the line is parallel to the y-axis then the y-coordinate will be zero.
mx+b = 0
x=-b/m
Slope: The slope of the line is equal to the ratio of the change in y-coordinates to the change in x-coordinates. It can be evaluated by:
m = (y2-y1)/(x2-x1)
So basically the slope shows the rise of line in the plane along with the distance covered in the x-axis. The slope of the line is also called a gradient.
Point Slope Form
In this form of linear equation, a straight line equation is formed by considering the points in the x-y plane, such that:
y – y1 = m(x – x1 )
where (x1, y1) are the coordinates of the point.
We can also express it as:
y = mx + y1 – mx1
Summary:
There are different forms to write linear equations. Some of them are:
| Linear Equation | General Form | Example |
| Slope intercept form | y = mx + b | y + 2x = 3 |
| Point–slope form | y – y1 = m(x – x1 ) | y – 3 = 6(x – 2) |
| General Form | Ax + By + C = 0 | 2x + 3y – 6 = 0 |
| Intercept form | x/a + y/b = 1 | x/2 + y/3 = 1 |
| As a Function | f(x) instead of y
f(x) = x + C |
f(x) = x + 3 |
| The Identity Function | f(x) = x | f(x) = 3x |
| Constant Functions | f(x) = C | f(x) = 6 |
Where m = slope of a line; (a, b) intercept of x-axis and y-axis.
Also, read:
How to Solve Linear Equations?
By now you have got an idea of linear equations and their different forms. Now let us learn how to solve linear equations or line equations in one variable, in two variables and in three variables with examples. Solving these equations with step by step procedures are given here.
Solution of Linear Equations in One Variable
Both sides of the equation are supposed to be balanced for solving a linear equation. The equality sign denotes that the expressions on either side of the ‘equal to’ sign are equal. Since the equation is balanced, for solving it, certain mathematical operations are performed on both sides of the equation in a manner that does not affect the balance of the equation. Here is the example related to the linear equation in one variable.
Example: Solve (2x – 10)/2 = 3(x – 1)
Step 1: Clear the fraction
x – 5 = 3(x – 1)
Step 2: Simplify Both sides equations
x – 5 = 3x – 3
x = 3x + 2
Step 3: Isolate x
x – 3x = 2
Solution of Linear Equations in Two Variables
To solve linear equations in 2 variables, there are different methods. Following are some of them:
We must choose a set of 2 equations to find the values of 2 variables. Such as ax + by + c = 0 and dx + ey + f = 0, also called a system of equations with two variables, where x and y are two variables and a, b, c, d, e, f are constants, and a, b, d and e are not zero. Else, the single equation has an infinite number of solutions.
Solution of Linear Equations in Three Variables
To solve linear equations in 3 variables, we need a set of 3 equations as given below to find the values of unknowns. Matrix method is one of the popular methods to solve system of linear equations with 3 variables.
a1x + b1 y + c1z + d1 = 0
a2x + b2 y + c2 z + d2 = 0 and
a3x + b3 y + c3 z + d3 = 0
Also check: Solve The Linear Equation In Two Or Three Variables
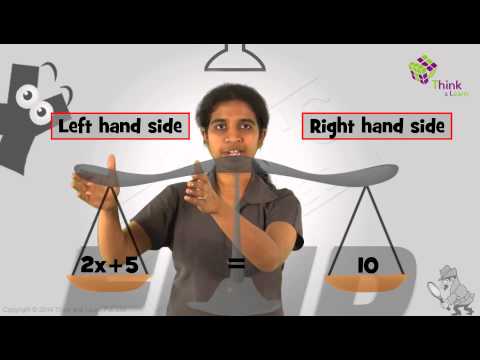
Solving Linear Equations
Example 1:
Solve x = 12(x +2)
Solution:
x = 12(x + 2)
x = 12x + 24
Subtract 24 on both sides of equation
x – 24 = 12x + 24 – 24
x – 24 = 12x
Simplify
11x = -24
Isolate x:
x = -24/11.
Example 2:
Solve x – y = 12 and 2x + y = 22
Solution:
Name the equations
x – y = 12 …(1)
2x + y = 22 …(2)
Isolate Equation (1) for x,
x = y + 12
Substitute x =y + 12 in equation (2)
2(y+12) + y = 22
3y + 24 = 22
3y = -2
or y = -2/3
Substitute the value of y in x = y + 12
x = y + 12
x = -2/3 + 12
x = 34/3
Practice Questions
Solve the following linear equations:
- 5y-11=3y+9
- 3x + 4 = 7 – 2x
- 9 – 2(y – 5) = y + 10
- 5(x – 1) = 3(2x – 5) – (1 – 3x)
- 2(y – 1) – 6y = 10 – 2(y – 4)
- y/3 – (y – 2)/2 = 7/3
- (y – 3)/4 + (y – 1)/5 – (y – 2)/3 = 1
- (3x – 2)/3 + (2x + 3)/3 = (x + 7)/6
- (8y – 5)/(7y + 1) = -4/5
- (5 – 7y)/(2 + 4y) = -8/7
Stay tuned with BYJU’S – The Learning App and download the app to learn all Maths concepts and also get the video lesson to learn the concepts quickly.
Frequently Asked Questions on Linear Equations
What is a Linear equation?
What are the three forms of linear equations?
How do we express the standard form of a linear equation?
Ax + By + C = 0
Here, A, B and C are constants, x and y are variables.
Also, A ≠ 0, B ≠ 0
What is the slope-intercept form of linear equations?
y=mx+b
Where m denotes the steepness of line and b is the y-intercept.
What is the difference between linear and non-linear equations?
A non-linear equation does not form a straight line. It can be a curve that has a variable slope value.