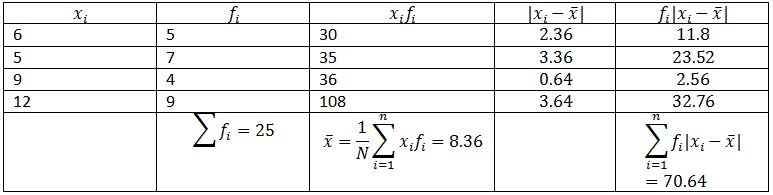Mean Deviation
In statistics and mathematics, the deviation is a measure that is used to find the difference between the observed value and the expected value of a variable. In simple words, the deviation is the distance from the center point. Similarly, the mean deviation is used to calculate how far the values fall from the middle of the data set. In this article, let us discuss the definition, formula, and examples in detail.
Table of Contents:
Mean Deviation Definition
The mean deviation is defined as a statistical measure that is used to calculate the average deviation from the mean value of the given data set. The mean deviation of the data values can be easily calculated using the below procedure.
Step 1: Find the mean value for the given data values
Step 2: Now, subtract the mean value from each of the data values given (Note: Ignore the minus symbol)
Step 3: Now, find the mean of those values obtained in step 2.
Mean Deviation Formula
The formula to calculate the mean deviation for the given data set is given below.
Mean Deviation = [Σ |X – µ|]/N
Here,
Σ represents the addition of values
X represents each value in the data set
µ represents the mean of the data set
N represents the number of data values
| | represents the absolute value, which ignores the “-” symbol
Mean Deviation for Frequency Distribution
To present the data in the more compressed form we group it and mention the frequency distribution of each such group. These groups are known as class intervals.
Grouping of data is possible in two ways:
- Discrete Frequency Distribution
- Continuous Frequency Distribution
In the upcoming discussion, we will be discussing mean absolute deviation in a discrete frequency distribution.
Let us first know what is actually meant by the discrete distribution of frequency.
Mean Deviation for Discrete Distribution Frequency
As the name itself suggests, by discrete we mean distinct or non-continuous. In such a distribution the frequency (number of observations) given in the set of data is discrete in nature.
If the data set consists of values x1,x2, x3………xn each occurring with a frequency of f1, f2… fn respectively then such a representation of data is known as the discrete distribution of frequency.
To calculate the mean deviation for grouped data and particularly for discrete distribution data the following steps are followed:
Step I: The measure of central tendency about which mean deviation is to be found out is calculated. Let this measure be a.
If this measure is mean then it is calculated as,
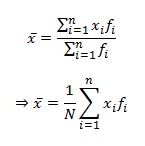
where \(N=\sum_{i=1}^{n}\;f_{i}\)
If the measure is median then the given set of data is arranged in ascending order and then the cumulative frequency is calculated then the observations whose cumulative frequency is equal to or just greater than N/2 is taken as the median for the given discrete distribution of frequency and it is seen that this value lies in the middle of the frequency distribution.
Step II: Calculate the absolute deviation of each observation from the measure of central tendency calculated in step (I)
StepIII: The mean absolute deviation around the measure of central tendency is then calculated by using the formula
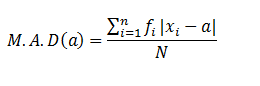
If the central tendency is mean then,
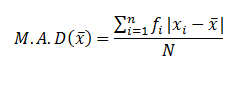
In case of median
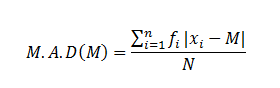
Let us look into the following examples for a better understanding.
Read: Mean Deviation for Continous Frequency Distribution
Mean Deviation Examples
Example 1:
Determine the mean deviation for the data values 5, 3,7, 8, 4, 9.
Solution:
Given data values are 5, 3, 7, 8, 4, 9.
We know that the procedure to calculate the mean deviation.
First, find the mean for the given data:
Mean, µ = ( 5+3+7+8+4+9)/6
µ = 36/6
µ = 6
Therefore, the mean value is 6.
Now, subtract each mean from the data value, and ignore the minus symbol if any
(Ignore”-”)
5 – 6 = 1
3 – 6 = 3
7 – 6 = 1
8 – 6 = 2
4 – 6 = 2
9 – 6 = 3
Now, the obtained data set is 1, 3, 1, 2, 2, 3.
Finally, find the mean value for the obtained data set
Therefore, the mean deviation is
= (1+3 + 1+ 2+ 2+3) /6
= 12/6
= 2
Hence, the mean deviation for 5, 3,7, 8, 4, 9 is 2.
Example 2:
In a foreign language class, there are 4 languages, and the frequencies of students learning the language and the frequency of lectures per week are given as:
| Language | Sanskrit | Spanish | French | English |
| No. of students(xi) | 6 | 5 | 9 | 12 |
| Frequency of lectures(fi) | 5 | 7 | 4 | 9 |
Calculate the mean deviation about the mean for the given data.
Solution: The following table gives us a tabular representation of data and the calculations
Frequently Asked Questions on Mean Deviation
What does the mean deviation tell us?
The mean deviation gives information about how far the data values are spread out from the mean value.
Mention the procedure to find the mean deviation.
The procedure to find the mean deviation are:
Step 1: Calculate the mean value for the given data
Step 2: Subtract the mean from each data value (Distance)
Step 3: Finally, find the mean for the distance
What are the advantages of using the mean deviation?
The advantages of using mean deviation are:
It is based on all the data values provided, and hence it will give a better measure of dispersion.
It is easy to understand and calculate.
What is the mean deviation about a median?
The mean deviation about the median is similar to the mean deviation about mean. Instead of calculating the mean for the given set of data values, find the median value by arranging the data values in the ascending order and then find the middle value. After finding the median, now subtract the median from each data value, and finally, take the average
What are the three different ways to find the mean deviation?
The mean deviation can be calculated using
Individual Series
Discrete series
Continuous series