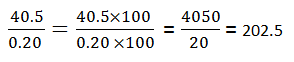Multiplication And Division Of Decimals
In Mathematics, multiplication and division are the two important arithmetic operations. Both the multiplication and division operations are closely related to each other just like addition and subtraction. All these operations are performed on all real numbers. The rules for multiplication and division of integers differ from rules for fractions and decimals.
Let us learn more about multiplication and division along with rules and examples. Also, learn how to multiply and divide integers, fractions and decimals.
| Table of Contents: |
What is Multiplication and Division in Maths?
In mathematics, there are four basic operations.
- Addition (+)
- Subtraction (-)
- Multiplication (×)
- Division (÷)
What is Multiplication?
Multiplication is the repeated addition of a number. If we multiply m by n, that means m is repeatedly added to itself for n times. The symbol for multiplication is ‘×’.
For instance, 8 multiplied by 4 is equal to 32. How? Adding 8, 4 times to itself, we get;
8 + 8 + 8 + 8 = 32
Therefore, we can write,
8 x 4 = 32
What is Division?
The division is a method of dividing or distributing a number into equal parts, For example, if 16 is divided by 4, then 16 is divided into 4 equal parts. Therefore, the resultant value is 4.
16 ÷ 4 = 4
Parts of division
Dividend ÷ Divisor = Quotient
15 ÷ 3 = 5
In the above example, there are three parts for division.
- 15 is dividend
- 3 is divisor
- 5 is quotient (R.H.S)
Multiplication and Division Relationship
Multiplication and division, are inverse operations of each other. If we say, a multiplied by b is equal to c, then c divided by b results in a. Mathematically, it can be represented as:
- a × b = c
- c ÷ b = a
For example,
- 4 x 5 = 20 [4 multiplied by 5 results in 20]
- 20 ÷ 5 = 4 [20 divided by 5 returns back 4]
Multiplication and Division Rules
For every mathematical computation, we need to follow the rules. Thus even to multiply and divide the numbers, there are some rules which we need to follow.
Rule 1: Order of operations
The order of operations for multiplication does not matter. It means if we arrange the number in a different order while multiplying them, then the result will be the same.
Examples are:
3 x 4 = 12
4 x 3 = 12
In the above example, we can see, even if we have swapped the position of 3 and 4, the product of the two integers is equal to 12.
But this rule is not applicable for division. Let us take another example.
12 ÷ 3 = 4
3 ÷ 12 ≠ 4 (it is equal to 0.25)
Thus, we cannot change the order of numbers in division method.
Rule 2: Multiplying and Dividing by Positive Numbers
If any real number is multiplied or divided by the positive real number, then the sign of the resulting number does not change.
Examples are:
2 x 3 = 6
-2 x 3 = -6
Since, 2 and 3 both are positive integers, therefore the product of 2 and 3 is also positive. But the product of -2 and 3 is a negative number.
4 ÷ 2 = 2
-4 ÷ 2 = -2
Since, 4 and 2 both are positive, therefore, 4 divided by 2 is also a positive number. But -4 divided by 2 is a negative number.
Thus, we can conclude that:
|
Rule 3: Multiplying and Dividing by Negative Numbers
Multiplication and division of any real number by a negative number will change the sign of the resulting number. Examples are given below.
- Multiply 5 by -2.
5 x -2 = -10
- Multiply -5 by -2.
-5 x -2 = 10
- Divide 10 by 2.
10 ÷ -2 = -5
-10 ÷ -2 = 5
Thus we can conclude that:
|
Summary of Multiplication and Division Rules
| Multiplication rules | Division rules |
|
|
Multiplication and Division of Integers
Integers are those values that are not fractions and can be negative, positive or zero. The integers can be easily represented on a number line. Thus, the arithmetic calculations on integers can be done in a simple manner.
Multiplying and dividing any integer with a whole number, or a fraction or an integer itself is given below with examples.
- 3 x 9 = 27 (Integer x Whole number)
- 2 x ¼ = ½ (Integer x Fraction)
- 2 x -5 = -10 (Integer x Integer)
Multiplication and Division of Fractions
Here, we will learn how to multiply and divide fractions with examples.
A fraction is a part of a whole. For example, ½ is a fraction that represents half of a whole number or any value. Here, the upper part is called the numerator and the lower part is called the denominator. Let us multiply and divide fractions with examples.
¼ x ½ = (1 x 1)/(4 x 2) = ⅛
¼ ÷ ½ = (1 x 2)/(1 x 4) = 2/4 = ½
Multiplication and Division of Decimals
Decimals are numbers with a decimal point, (Eg: 2.35). They represent the fraction of something or some value, such as ½ = 0.5. A decimal notation or point differentiates an integer part from fractional part (e.g. 2.35 = 2 + 7/20).
Multiplication of Decimals
When a decimal is multiplied by any real number, then the position of the decimal point (.) changes.
For example: 0.33 x 2= 0.33 + 0.33 + 0.33. Multiplication of decimal numbers is similar to the multiplication of whole numbers. Steps for multiplication of decimals are given below with an example.
Consider multiplication of two numbers, 2.32 and 3 for example.
Step 1: Take the count of the total number of places (digits) to the right of the decimal point in both numbers.
Here, in 2.32 there are two digits to the right of the decimal point and 3 is a whole number with no decimal point. Therefore, the total number of digits to the right of the decimal is 2.
Step 2: Now forget about the decimal point and just multiply the numbers without the decimal point.
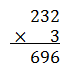
Step 3: After multiplication, put the decimal point in answer 2 places (step 1) from the right i.e. answer (2.32 x 3) will be 6.96.
Simply, just multiply the decimal numbers without decimal points and then give decimal point in the answer as many places same as the total number of places right to the decimal points in both numbers.
Division of Decimals
We can use the same trick we used in the multiplication of decimals i.e. remove the decimal points and divide the numbers like whole numbers.
Let’s divide 40.5 by .20. Methods to divide these decimal numbers are as follows:
Method 1: Convert the decimal numbers into whole numbers by multiplying both numerator and denominator by the same number. The denominator must be always a whole number.
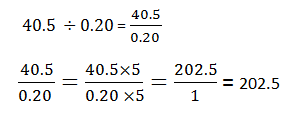
(Multiply both the numerator and denominator by 5)
Method 2: Alternatively, one can convert decimal numbers into whole numbers by multiplying with numbers having powers of 10 (10, 100, 1000, etc.).
- Consider the denominator, count the number of places (digits) right to the decimal point.
Here, the denominator is 0.20 and the number of digits right to the decimal point is 2.
40.5 ÷ 0.20 = 40.5 / 0.20
- Take the power of 10 the same as the number of digits right to the decimal point e. 102 = 100
- Multiply both numerator and denominator by 100.
Multiplication and Division of Decimal Numbers by 10, 100 and 1000
Multiplication and division of decimals by numbers that have powers of 10 is easier than that by a whole number. Rules for multiplication and division of decimal numbers by 10, 100 and 1000:
| Multiplication and Division | Rules | Examples |
| Multiply by 10
(101) |
the number will move one place value to the left | 5.63 x 10 =56.3 |
| Multiply by 100 (102) | the number will move two places value to the left | 5.63 x 100 =563 |
| Multiply by 1000 (103) | the number will move three places value to the left | 5.63 x 1000 =5630 |
| Divide by 10
(101) |
the number will move one place value to the right | 56.3 ÷ 10 =5.63 |
| Divide by 100
(102) |
the number will move two places value to the right | 56.3 ÷ 100 =0.563 |
| Divide by 1000
(103) |
the number will move three places value to the right | 56.3 ÷ 1000 =0.0563 |
Multiplication and Division Equations
The equations are the expression that includes integers, variables, equality signs and arithmetic operations. For example,
2a + 9 = 7
If we solve the above equation for a, then,
2a = 7 – 9
a = -2÷2 = -1
Thus, we can see, the above solution involved both multiplication and division methods.
Related Articles
- Multiplication of fractions
- Division of fractions
- Addition and Subtraction of Decimals
- Addition And Subtraction Of Integers
- Multiplication Tables
- Multiplication Tricks
Solved Examples – Multiplication and Division
Q.1: Find the product of:
- 22 x 11 = ?
- 3 x 91 = ?
- 444 x 3 = ?
- 1000 x 8 = ?
Solution:
- 22 x 11 = 242
- 3 x 91 = 273
- 444 x 3 = 1332
- 1000 x 8 = 8000
Q.2: Find the division of:
- 34 ÷ 2 = ?
- 555 ÷ 5 = ?
- 81 ÷ 3 = ?
- 812 ÷ 4 = ?
Solution: The divisions are:
- 34 ÷ 2 = 17
- 555 ÷ 5 = 111
- 81 ÷ 3 = 27
- 812 ÷ 4 = 203
Word Problems on Multiplication and Division
Q.1: There are 90 pencils in 1 box. How many pencils are there in 3 boxes?
Solution: Given, 1 box has 90 pencils.
So, in 3 boxes, number of pencils = 3 x 90 = 270
Therefore, there are total of 270 pencils in 3 boxes.
Q.2: Raju has 1615 candies stored in a box. If there are 85 such boxes, then how many candies are there in each box?
Solution: Total number of candies = 1615
Number of boxes = 85
Therefore, each box contains = 1615 ÷ 85 candies
Practice Questions – Multiplication and Division
1. Fill in the blanks:
- 7 x 9 = ___
- 83 ÷ 2 = __
2. Find the value of:
- ⅔ x 5/9 = ?
- ⅚ x 12 = ?
- 16 ÷ 4/3 = ?
- 200 ÷ 40 = ?
3. Each toffee cost Rs. 2. If there are 120 toffees, then what is the total cost?
4. A school is planning a trip. There are 1729 students and each bus has 19 seats. How many buses are required to go for the trip?
To solve more problems on multiplication and division of decimals, download BYJU’S – The Learning App from Google Play Store and watch interactive videos.
Frequently Asked Questions on Multiplication and Division
What is the order of operations of multiplication and division?
15 ÷ 3 x 2 = 5 x 2 = 10
15 ÷ (3 x 2) = 15 ÷ 6 = 2.5
What do we get when we multiply an integer with an integer?
Integer x Integer = Integer
How do you divide a number by a fraction?
3 ÷ (⅓)
Reciprocal of ⅓ is 3
Therefore,
3 x 3 = 9.
How to multiply decimal by a fraction?
0.5 x ⅓
0.5 = 5/10 = ½
½ x ⅓ = ⅙