Perpendicular Bisector
A perpendicular bisector can be defined as a line that intersects another line segment perpendicularly and divides it into two parts of equal measurement. We can draw a perpendicular bisector using a rule, a compass and a pencil.
Two lines are said to be perpendicular to each other when they intersect each other at 90 degrees or at right angles. And, a bisector is a line that divides a line into two equal halves. Thus, a perpendicular bisector of a line segment AB implies that it intersects AB at 90 degrees and cuts it into two equal halves.
What is a Perpendicular Bisector?
A perpendicular bisector is a line that bisects another line segment at a right angle, through the intersection point. Thus, we can say, a perpendicular bisector always divides a line segment through its midpoint. The term bisect itself means dividing equally or uniformly.
Properties of a Perpendicular Bisector
- It divides AB into two equal halves or bisects it.
- It makes right angles with (or is perpendicular to) AB.
- Every point in the perpendicular bisector is equidistant from point A and B.
While working with practical geometry, you will often find the application of perpendicular bisectors; say when you are asked to draw an isosceles triangle, or when you have to determine the centre of a circle, etc. Below are the steps to construct a perpendicular bisector of a line using a compass and a ruler.
How to Construct a Perpendicular Bisector?
You will require a ruler and compasses. The steps for the construction of a perpendicular bisector of a line segment are:
- Step 1: Draw a line segment PQ.
- Step 2: Adjust the compass with a length of a little more than half of the length of PQ.
- Step 3: Place the compass pointer at point P and draw arcs above and below the line.
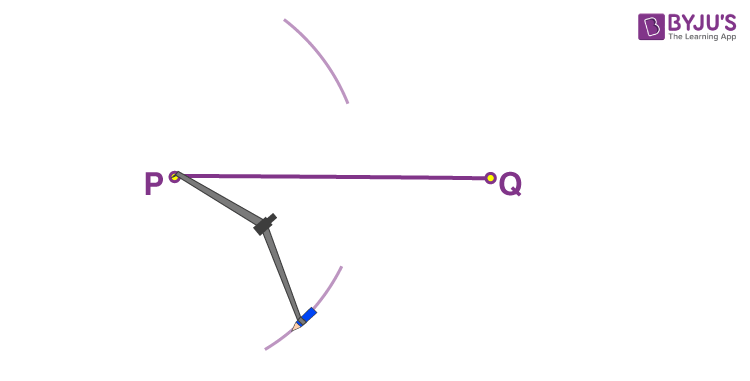
- Step 4: Keeping the same length in the compass, place the compass pointer at point Q. Similarly, draw two arcs above and below the line keeping the compass pointer at Q.
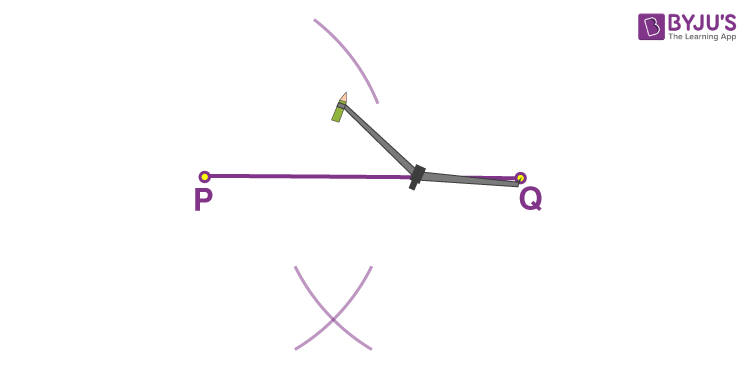
- Step 5: Mark the points where the opposite arcs cross as X and Y.
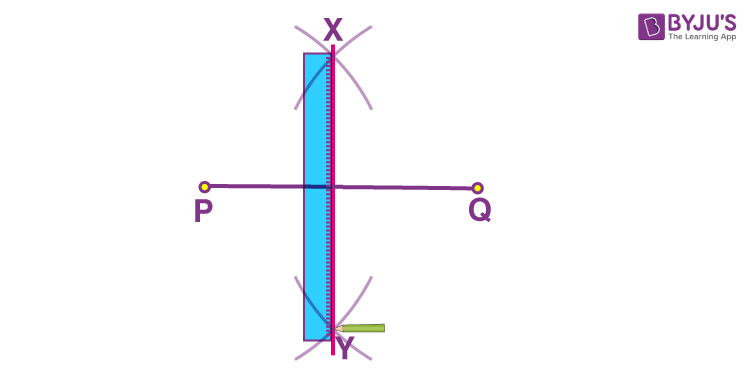
- Step 6: Using a ruler, draw a line passing across X and Y.
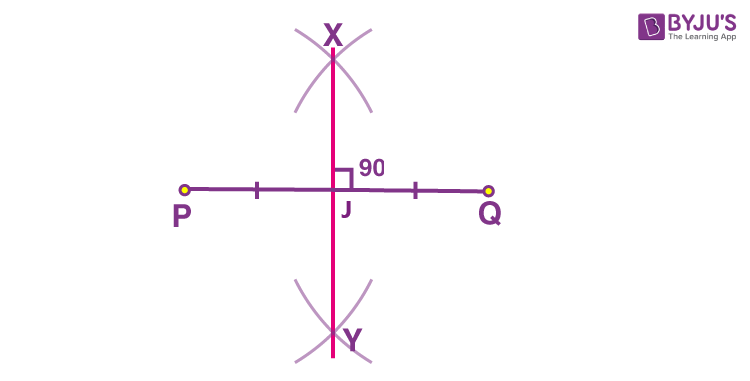
The perpendicular bisector bisects PQ at a point J, that is, the length PJ is equal to JQ. And the angle between the two lines is 90 degrees.
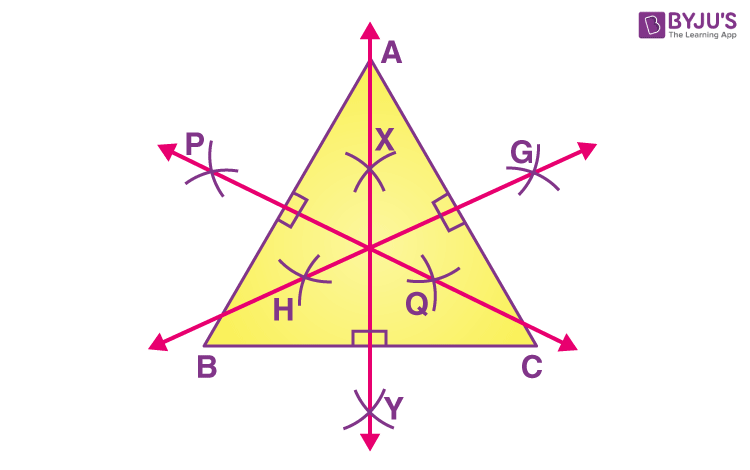
Perpendicular Bisector of Triangles
The perpendicular bisector of a triangle is the line segment that is drawn from a vertex to the opposite side bisecting the side at a right angle. The perpendicular of a triangle is perpendicular to the sides drawn from the opposite vertices and divides the sides into two equal parts. The point at which all the three perpendicular bisectors of a triangle meets is called the circumcenter of a triangle.
Related Articles
| Perpendicular Lines | Construction of Perpendicular Line Through a Point |
| Construction Of Perpendicular Lines | Angle Between Two Lines |
| Bisector | Angle Bisectors |
Solved Examples
Q.1: If a line segment is of length equal to 8cm and a perpendicular bisector is drawn to it. What is the measure of each part of the line segment?
Solution: By the definition, we know, a perpendicular bisector intersects a line segment at the right angle and divides it into two equal parts.
Hence, the measure of each part of the line segment (8 cm), which is bisected by a perpendicular is 4 cm.
Q.2: Can we draw a perpendicular bisector, if the length of the radius of a circle is known?
Solution: Yes, we can draw the perpendicular bisector if we know the radius of the circle. Since the diameter of a circle is equal to twice of radius. Hence. we can draw a perpendicular bisector to the diameter of circle following the same steps.
Practice Questions
- Draw a perpendicular bisector to a line segment equal to 12 cm.
- Construct a perpendicular bisector of a line segment equal to 6.6 cm.
Frequently Asked Questions on Perpendicular Bisector
What does a Perpendicular Bisector Mean?
A perpendicular bisector can be defined as a line segment which bisects another line segment at 90 degrees. In other words, a perpendicular bisector intersects another line segment at 90° and divides it into two equal parts.
Can a Perpendicular Bisector be a Median of a Triangle?
Yes, a perpendicular bisector can be a median of a triangle. A median is defined as a line segment from a vertex of a triangle to the midpoint of the side opposite that vertex. So, if the median joins the opposite side at 90 degrees, it will be the perpendicular bisector of that side. For example, for an equilateral triangle, the medians are always perpendicular bisectors.
What is the Point at Which the Perpendicular Bisectors of a Triangle Meet Called?
The point at which the perpendicular bisectors of a triangle meet are known as the circumcenter of the triangle and it is equidistant from all the vertices.
What is Perpendicular Bisector Theorem?
Perpendicular bisector theorem states that if a point is on the perpendicular bisector of a segment, then it is equidistant from the segment’s endpoints.