When each point on a plane of a two-dimensional coordinate system is decided by a distance from a reference point and an angle is taken from a reference direction, it is known as the polar coordinate system.

Pole = The reference point

Polar axis = the line segment ray from the pole in the reference direction

In the polar coordinate system, the origin is called a pole.

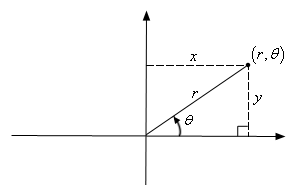
Here, instead of representing the point as (x, y), we can express it as a polar coordinate (r, θ).

Where the value of r can be negative. The value of angle changes based on the quadrant in which the r lies.

Read more:

• Coordinate Geometry
• Coordinates of a Point in Three Dimensions
• Coordinate Geometry Class 9 Notes
• Coordinate Geometry Class 10 Notes

The above information can be tabulated as below:https://byjus.com/biology/icse-articles-biology/

Note:

In the Cartesian coordinate system, the distance of a point from the y-axis is called its x-coordinate and the distance of a point from the x-axis is called its y-coordinate.

Polar grid

Polar grid with different angles as shown below:

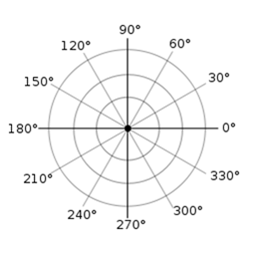
Also, π radians are equal to 360°.

Polar Coordinates Formula

We can write an infinite number of polar coordinates for one coordinate point, using the formula

(r, θ+2πn) or (-r, θ+(2n+1)π), where n is an integer.

The value of θ is positive if measured counterclockwise.

The value of θ is negative if measured clockwise.

The value of r is positive if laid off at the terminal side of θ.

The value of r is negative if laid off at the prolongation through the origin from the terminal side of θ.

Note:

The side where the angle starts is called the initial side and the ray where the measurement of the angle stops is called the terminal side.

Cartesian to Polar Coordinates

x = r cos θ

y = r sin θ

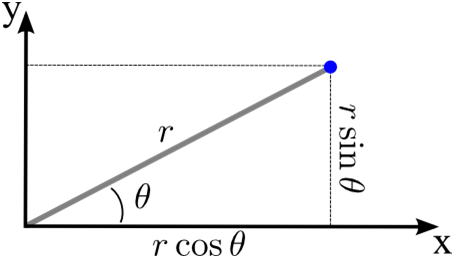
Finding r and θ using x and y:

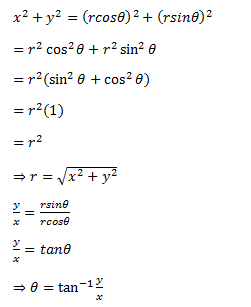
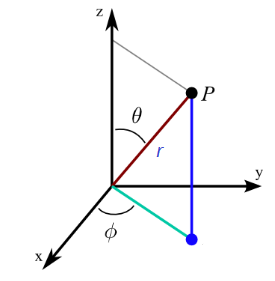
3D Polar Coordinates

3d polar coordinates or spherical coordinates will have three parameters: distance from the origin and two angles.

The 3d-polar coordinate can be written as (r, Φ, θ).

Here,

R = distance of from the origin

Φ = the reference angle from XY-plane (in a counter-clockwise direction from the x-axis)

θ = the reference angle from z-axis

Polar Coordinates Examples

Example 1:

Convert the polar coordinate (4, π/2) to a rectangular point.

Solution:

Given,

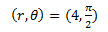
We know that,

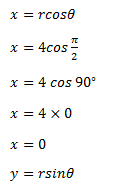
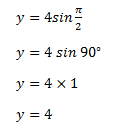
Hence, the rectangular coordinate of the point is (0, 4).

Example 2:

Convert the rectangular or cartesian coordinates (2, 2) to polar coordinates.

Solution:

Given,

(x, y)=(2, 2)

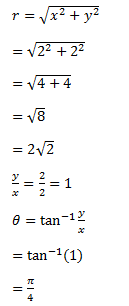
Note:

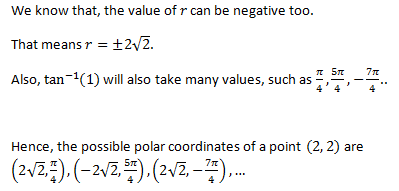
Polar Coordinates Applications

Two-dimensional polar coordinates play a significant role in navigation either on sea or in air.

If equations are expressed in polar coordinates, then calculus can be applied.