Properties of Isosceles Triangle
An isosceles triangle definition states it as a polygon that consists of two equal sides, two equal angles, three edges, three vertices and the sum of internal angles of a triangle equal to 1800. In this section, we will discuss the properties of isosceles triangle along with its definitions and its significance in Maths.
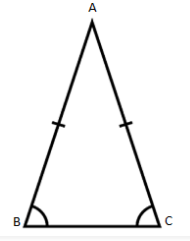
Apart from the isosceles triangle, there is a different classification of triangles depending upon the sides and angles, which have their own individual properties as well. Below is the list of types of triangles;
- Scalene Triangle
- Equilateral Triangle
- Acute angled Triangle
- Right angle Triangle
- Obtuse-angled Triangle
Isosceles triangle basically has two equal sides and angles opposite to these equal sides are also equal. Same like the Isosceles triangle, scalene and equilateral are also classified on the basis of their sides, whereas acute-angled, right-angled and obtuse-angled triangles are defined on the basis of angles. So before, discussing the properties of isosceles triangles, let us discuss first all the types of triangles.
Below are basic definitions of all types of triangles:
Scalene Triangle: A triangle which has all the sides and angles, unequal.
Equilateral Triangle: A triangle whose all the sides are equal and all the three angles are of 600.
Acute Angled Triangle: A triangle having all its angles less than right angle or 900.
Right Angled Triangle: A triangle having one of the three angles as right angle or 900.
Obtuse Angled Triangle: A triangle having one of the three angles as more than right angle or 900.
Isosceles Triangle Properties
An Isosceles Triangle has the following properties:
- Two sides are congruent to each other.
- The third side of an isosceles triangle which is unequal to the other two sides is called the base of the isosceles triangle.
- The two angles opposite to the equal sides are congruent to each other. That means it has two congruent base angles and this is called an isosceles triangle base angle theorem.
- The angle which is not congruent to the two congruent base angles is called an apex angle.
- The altitude from the apex of an isosceles triangle bisects the base into two equal parts and also bisects its apex angle into two equal angles.
- The altitude from the apex of an isosceles triangle divides the triangle into two congruent right-angled triangles.
- Area of Isosceles triangle = ½ × base × altitude
- Perimeter of Isosceles triangle = sum of all the three sides
Example: If an isosceles triangle has lengths of two equal sides as 5 cm and base as 4 cm and an altitude are drawn from the apex to the base of the triangle. Then find its area and perimeter.
Solution: Given the two equal sides are of 5 cm and base is 4 cm.
We know, the area of Isosceles triangle = ½ × base × altitude
Therefore, we have to first find out the value of altitude here.
The altitude from the apex divides the isosceles triangle into two equal right angles and bisects the base into two equal parts. Thus, by Pythagoras theorem,
Hypotenuse2 = Base2 + Perpendicular2
Or Perpendicular = \(\sqrt{Hypotenuse^2-Base^2}\)
∴ Altitude = \(\sqrt{5^2-2^2}\)
= \(\sqrt{25-4}\)
= √21
So, the area of Isosceles triangle = ½ × 4 × √21 = 2√21 cm2
Perimeter of Isosceles triangle = sum of all the sides of the triangle
= 5 + 4 +5 cm
= 14 cm
Get more of example questions based on geometrical topics only in BYJU’S. Also, download the BYJU’S app to get a visual of such figures and understand the concepts in a more better and creative way and learn more about different interesting topics of geometry.