Sin 0
In trigonometry, there are three major or primary function, Sine, Cosine and Tangent, which are used to find the angles and length of the right-angled triangle. Before discussing Sin 0, let us know about Sine function.
Sine function defines a relation between the angle and perpendicular side and hypotenuse side. Or you can sin theta (the angle formed between the hypotenuse and adjacent side) is equal to the ratio of perpendicular and hypotenuse of a right-angled triangle.
Let us discuss more of the trigonometric sine functions here in this article.
Sine Definition In Terms of Sin 0
As we have already discussed, the sin of angle theta is a ratio of the length of the opposite side, perpendicular and hypotenuse of the right-angled triangle.
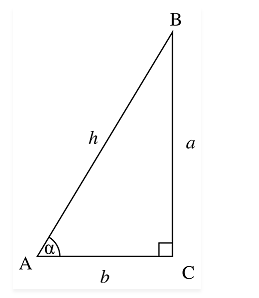
Sin \(\theta\) = \(\frac{Opposite Side}{Hypotenuse}\)
= \(\frac{Perpendicular}{Hypotenuse}\)
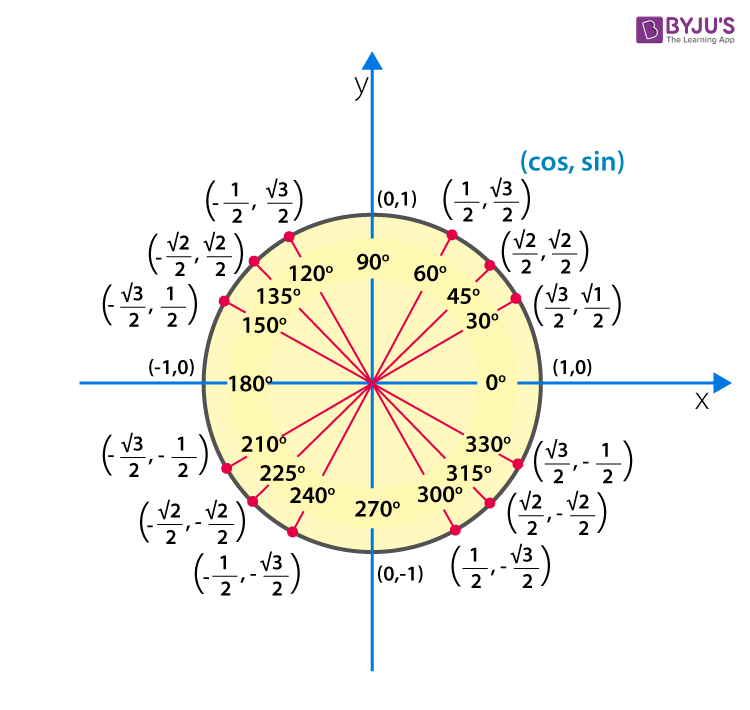
Now if we want to calculate sin 0 degrees value, we have to check the coordinates point on x and y plane. Sin 0 signifies that the value of x coordinate is 1 and the value of y coordinate is 0,i.e. (x,y) is (1,0). That means the value of the opposite side or perpendicular is zero and the value of hypotenuse is 1. So if we place the values in sin ratio for \(\theta\)=00 , perpendicular side= 1 and hypotenuse as 0, then we get,
Sin 00 =0/1
Or
Sin 00 = 0
From the above equation, we have yield sin 0 degrees value. Now let us write other sin degrees or radians values for one full revolution, in a table.
| Sine Degrees/Radians | Values |
| Sin 00 | 0 |
| Sin 300 or Sin π/6 | 1/2 |
| Sin 450 or Sin π/4 | \(1/\sqrt{2}\) |
| Sin 600 or Sin π/3 | \(\sqrt{3}/2\) |
| Sin 900 or Sin π/2 | 1 |
| Sin 180°c or Sin π | 0 |
| Sin 270° or Sin 3π/2 | -1 |
| Sin 360° or Sin 2π | 0 |
If we write opposite of the value of Sin degrees, we get the values of cos degrees. Because, Sin \(\theta\)=1/Cos\(\theta\)
Therefore we can write,
Sin 00= Cos 900=0
Sin 300=Cos 600=½
Sin 450=Cos 450 = \(1/\sqrt{2}\)
Sin 600=Cos 300=\(\sqrt{3}/2\)
Sin 900=Cos 00=1
In the same way, we can write the values for Tan degrees.
Tan \(\theta\)=Sin\(\theta\)/Cos\(\theta\)
Therefore,
Tan 00=Sin 00/Cos 00=0
Tan 300=Sin 300/Cos 300=\(\sqrt{3}\)/2
Tan 450=Sin 450/Cos 450=1
Tan 600=Sin 600/Cos 600=\(\sqrt{3}\)
Tan 900=Sin 900/Cos 900=Undefined
We learned about sin theta 0 degrees value along with other degree values here, this far. Also, derived the value for cos degree and tan degrees with respect sin degrees. In the same way, we can find other trigonometric ratios like sec, cosec and cot.
Based on these values, we can draw the trigonometry table,
| Angle | 00 | 300 | 450 | 600 | 900 | 1800 | 2700 | 3600 |
| Sin A | 0 | 1/2 | \(1/\sqrt{2}\) | \(\sqrt{3}/2\) | 1 | 0 | -1 | 0 |
| Cos A | 1 | \(\sqrt{3}/2\) | \(1/\sqrt{2}\) | 1/2 | 0 | -1 | 0 | 1 |
| Tan A | 0 | 1/\(\sqrt{3}\) | 1 | \(\sqrt{3}\) | Undefined | 0 | Undefined | 0 |
Example: Find the value of Sin 900+Cos 900
Solution: As we know, Sin 900=1
And Cos 900=0
Therefore, Sin 900+Cos 900 = 1+0 = 1
Example: Find the value of Sin 270°+2Tan 450
Solution: Sin 270°= -1
And Tan 450=1
Therefore, Sin 270°+2Tan 450 = -1+2*1 = -1+2 = 1
Learn more about trigonometric functions and download BYJU’S-The Learning App for a better experience.
| MATHS Related Links | |
| Trigonometric Ratios of Complementary Angles | Trigonometric Functions |
| Trigonometric Ratios Of Standard Angles | Trigonometric Equations |