A square pyramid is a pyramid, in geometry, that has a square base and four lateral faces. A Pyramid is a polyhedron that has a base and 3 or greater triangular faces that meet at a point above the base (the apex). A square pyramid is a three-dimensional shape that has a total of five faces, hence called a pentahedron.  A most famous example of such a pyramid in real life is the Great Pyramid of Giza. On a small scale when we learn about pyramids, then we have to learn the other concepts related to them, such as volume of pyramid, area of the pyramid. In this article, we will learn the definition of a square pyramid, types, properties, surface area and volume formulas with many solved examples.

What is a Square Pyramid?

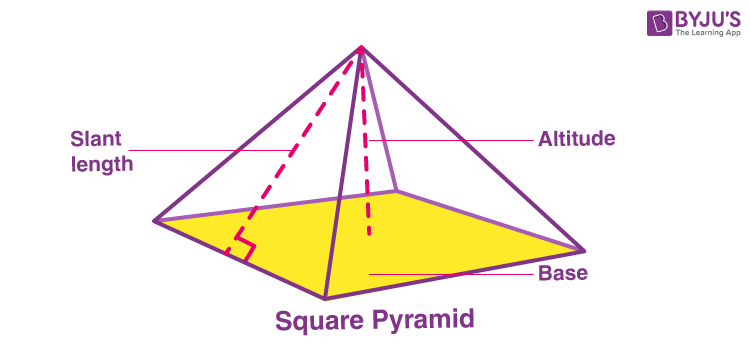
A three-dimensional geometric shape having a square base and four triangular faces/sides that meet at a single point (called vertex) is called a square pyramid. It is called a pentahedron, due to its five faces.  A square pyramid has:

• An apex: top vertex or point of the pyramid
• A Base in square shape
• Four triangular faces

If all the triangular faces have equal edges, then this pyramid is said to be an equilateral square pyramid.

If the apex of the pyramid is right above the centre of its base, it forms a perpendicular with the base and such a square pyramid is known as the right square pyramid.

All the pyramids are categorized based on their bases, such as:

• Rectangular pyramid
• Triangular pyramid
• Square pyramid
• Pentagonal pyramid
• Hexagonal pyramid

Properties of Square Pyramid

The properties of a square pyramid are:

• It has 5 Faces
• The 4 Side Faces are Triangles
• The Base is a Square
• It has 5 Vertices (corner points)
• It has 8 Edges

Representation of Square Pyramid

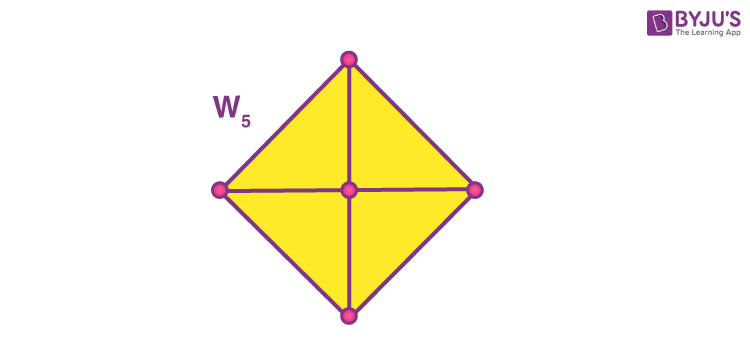
A square pyramid is shown by the Wheel graph W₅. A wheel graph is one formed by connecting a single universal vertex to all vertices of a cycle.

Types of Square Pyramid

The different types of square pyramids are :

• Equilateral Square Pyramid
• Right Square Pyramid
• Oblique Square Pyramid

Equilateral Square Pyramid

If all the edges are of equal length, then the sides form equilateral triangles, and the pyramid is an equilateral square pyramid.

The Johnson square pyramid can be classified by a single edge-length parameter l. The height h, the surface area A, and the volume V of such a pyramid are:

• h = (1/√2)l
• A = (1+√3)l²
• V = (√2/6)l³

Right Square Pyramid

In a right square pyramid, all the lateral edges are of the same length, and the sides other than the base are congruent isosceles triangles.

A right square pyramid with base length l and height h has the following formula for surface area and volume:

• \(Area=l^{2}+l\sqrt{l^{2}+(2h)^{2}}\)
• Volume=(⅓)×l²×h
• \(Lateral\ edge\ length =\sqrt{h^{2}+\frac{l^{2}}{2}}\)
• \(Slant\ Height = \sqrt{h^{2}+\frac{l^{2}}{4}}\)

Oblique Square Pyramid

If the apex of the square pyramid is not aligned with the center of the square base, then it is called an oblique square pyramid.

Square Pyramid Formula

There are formulas for square pyramid based on volume, surface area, height and base area. Find the formulas for:

• Volume of square pyramid
• Surface Area of square pyramid
• Lateral edge length
• Height of square pyramid

Volume of Square Pyramid

\(V = a^{2}\frac{h}{3}\)

Where a is the base edge length.

h is the height.

Base Area of square pyramid

The base of a square pyramid is a square. Therefore, here we can find the base area by finding the square of its edge-length.

Base area = side × side = edge²

Surface Area of a Square Pyramid

\(A = a^{2}+2a\sqrt{\frac{a^{2}}{4}+h^{2}}\)

Where a is the base edge length,

h is the height of square pyramid.

The general formula for the total surface area of a regular pyramid is given by:

T.S.A.= ½ Pl + B

where,

P is the perimeter of the base

l the slant height and

B the area of the base

Lateral Edge Length

\(e=\sqrt{h^{2}+\frac{l^{2}}{2}}\)

Where h is the height

And l is the base length

Height of square pyramid

\(e=\sqrt{h^{2}+\frac{l^{2}}{4}}\)

Where h is the height

And l is the base length

Net of a Square Pyramid

A net of a 3D shape is a pattern reached when the surface of a three-dimensional figure is laid out horizontally showing each face of the figure. A solid may have different nets.

The net of the square pyramid will give a flattened view, showing each and every face. When the net of the square pyramid is folded back, it will result in the original 3d shape.

Steps to determine whether net forms a solid are as follows:

1. Solid and the net should have the same number of faces. Also, the shapes of the faces of the solid should match with the shapes of the corresponding faces in the net.
2. Imagine how the net is to be folded to create the solid and assure that all the sides fit collectively properly.

Nets of the square pyramid are of use when we need to find its surface area.

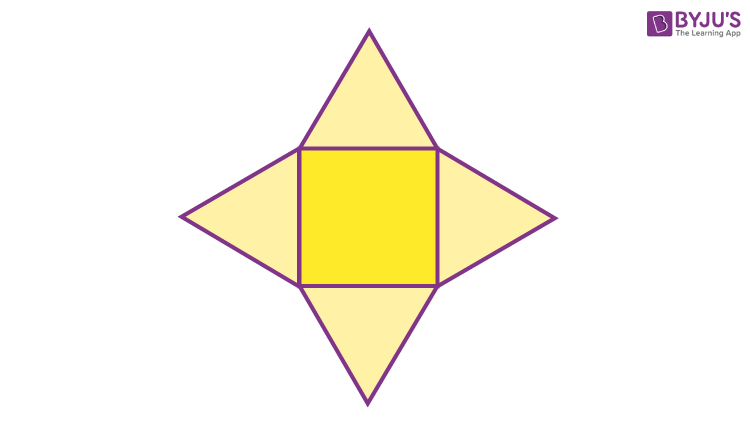
In the above net of a square pyramid, we can see, the shape is formed by one square and four triangles, attached with the four sides of the square. Hence, the surface area of the square pyramid will be the sum of the surface area of all its five faces.

Related Articles

• Pyramid
• Rectangular Pyramid
• Triangular Pyramid
• Volume of a Pyramid

Square Pyramid Solved Examples

Example 1:

Find the volume of a regular square pyramid with base sides 10 cm and altitude 18 cm.

Solution:

The formula for the volume of a square pyramid is given by:

V = ⅓ B h

As the base of the pyramid is a square, the base area is 10² or 100  cm².

So, put 100 for B and 18 for h in the formula.

V=13×100×18=600

Therefore, the volume of the given square pyramid is 600  cm³.

Example 2:

Find the lateral surface area of a regular pyramid that has a triangular base and each edge of the base is equal to 8 cms and the slant height is 5 cms.

Solution:

The perimeter of the base is the sum of the sides.

Perimeter = 3 × 8 = 24  cms

L.S.A.=12 × 24 × 5 = 60  cms²

Example 3:

Find the total surface area of a regular pyramid having a square base where the length of each edge of the base is equal to 16 cms, the slant height of a side is 17 cms and the altitude is 15 cms.

Solution:

The perimeter of the base is 4s because it is a square.

P = 4 × 16 = 64 cms

The area of the square base = s²

Base area = 16² = 256  cms²

Therefore, the total surface area of the pyramid,

T.S.A.=½ × 64 × 17 + 256  = 544 + 256  = 800  cms²