Square Root of 576
The value of the square root of 576 is equal to 24. In radical form, it is denoted as √576 = 24. To calculate the value to root 576 without using a calculator, there are two methods: one is the prime factorisation and another is the long division method. We will learn both the methods here, which will help students to find the root of any number easily and in the fastest way. Also, learn here about square root in a detailed way.
|
Square root of 576, √576 = 24 |
From the above expression, we can define the square root of 576, is a value (i.e. 24) which on multiplying by itself gives 576.
Hence, 24 x 24 = 576 or 242 = 576
Simplification of Square Root of 576
Here, we will learn to find the square root of 576 without using calculators, in two different ways.
Prime Factorisation:
In the prime factorisation method, we will write the prime factors of the given number. We have already learned in our previous classes, to find the prime factors of numbers. But, in the case of square roots, this method is applicable only if the given number is a perfect square.
Clearly, 576 is a perfect square, thus the prime factors are,
576 = 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3
Therefore, if we take the square root on both the sides, we get;
√576 = √2 × 2 × 2 × 2 × 2 × 2 × 3 × 3
As we can see here, there are three pairs of 2 and one pair of 3.
Hence,
√576 = 2 × 2 × 2 × 3
√576 = 24
Long Division method
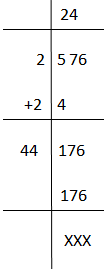
We can also find the square root of perfect squares using the long division method. This method is the fastest method to find the root of a number and is very useful to find the root of imperfect squares and large numbers. Below are the steps to find the value of √576 using the long division method.
- Take the first digit i.e. 5 and leave the rest two digits i.e. 76 for the division
- Now the square of 2 is 4. Therefore, taking 2 as divisor and 4 as quotient and 5 as dividend, we get remainder equal to 1.
- Now, we will take down the other two numbers, i.e. 76, as dividend and add 2 to the previous divisor to get our next divisor, i.e. 2+2 =4.
- Since the last digit is 6, then either the square of 4 or 6 can get the last digit as 6.
- Therefore, we will combine here 4 with 4 and multiply by 4 such as 44 x 4 to get 176
- Hence, the final quotient we get is 24, which is the actual answer.
Below are the solved steps to take the root of 576.
Find more square roots below: