In Mathematics, a step function (also called as staircase function) is defined as a piecewise constant function, that has only a finite number of pieces. In other words, a function on the real numbers can be described as a finite linear combination of indicator functions of given intervals. It is also called a floor function or greatest integer function. The step function is a discontinuous function. However, a mathematical definition of a step function is given below along with an example.

Step Function Definition

A step function f: R → R can be written in the form:

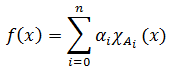
for all real numbers x.

If n ≥ 0, α_i are real numbers and A_i are intervals, then the indicator function of A is χ_A, and it can be written as below:

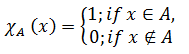
(Or)

A function f: R → R is called a step or greatest integer function if y = f(x) = [x] for x ∈ R.

Read more:

Definite Integral

Operations of Integers

Real Functions

Relations and Functions Class 11

Domain and Range

As we know, for any function domain is referred to as the set of input values that can be taken for an independent variable in the given function. Range of a function is defined as the set of output values generated for the domain (input values) of the function. In the case of a step function, for each value of x, f(x) takes the value of the greatest integer, less than or equal to x. For example:

[-2.19] = -3

[3.67] = 3

[-0.83] = -1

The domain of this function is a group of real numbers that are divided into intervals such as [-5, 3), [-4, 2), [-3, 1), [-2, 0) and so on. This explains the domain and range relations of a step function.

This can be generalized as given below:

[x] = -2, -2 ≤ x < -1

[x] = -1, -1 ≤ x < 0

[x] = 0, 0 ≤ x < 1

[x] = 1, 1 ≤ x < 2

Step Function Graph

The process of drawing a graph for a step function is similar to the graphing any piecewise function. Here, we need to graph each part of this function individually. The steps required to graph a step function are given below:

• First, draw a horizontal line segment at each constant output value throughout input values that it corresponds.
• The second step is to draw a closed circle point (a filled-in circle) at the included endpoint on each horizontal line that means if the end value is included in that interval, then it should be represented with a filled circle.
• Finally, draw an open circle point (a circle not filled in) at the endpoint that is excluded on each horizontal line. In other words, if the end value is not included in that interval, then it should be represented with an open circle.

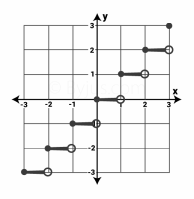
Thus, the graph of a step function is as shown below.

Step Function Example

Question 

Draw a graph of the step function:

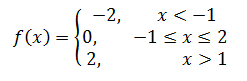
Solution:

From the given,

-2, 0, 2 are the values of y.

x < -1 means the values of x = …, -4, -3, -2, -1

-1 ≤ x ≤ 2 means, x = -1, 0, 1, 2

x > 1 means the values of x = 1, 2, 3, 4, …..

By plotting these values on a graph paper, the below graph will obtain.

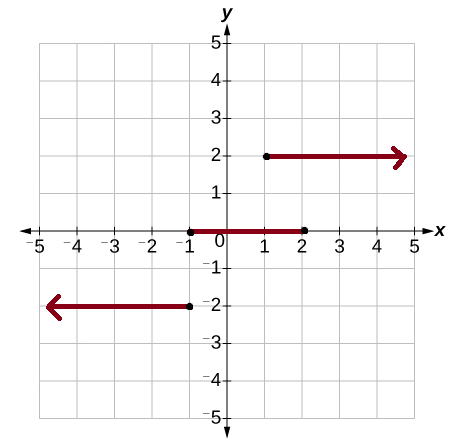
The above graph is viewed as a group of steps and hence it is also called a step function graph. The left endpoint in every step is blocked(dark dot) to show that the point is a member of the graph, and the other right end arrow indicates that the values are infinite. That means only definite values are shown with dark dots.

Properties

The important properties of step functions are given below:

• The sum or product of two-step functions is also a step function.
• If a step function is multiplied by a number, then the result produced is again a step function. That indicates the step functions create an algebra over the real numbers
• A step function can take only a finite number of values
• Piecewise linear function is the definite integral of a step function

One can observe step function when dealing with other types of functions for different reasons. For instance, a trivial example of a step function is a constant function. The simplest non-constant step function is sign function “sgn(x)”, because this function results -1 for the negative inputs and 1 (i.e. +1) for the positive input values. Other types include Heaviside function and rectangular function, etc.

To learn more about functions, types of functions and other maths concepts, download BYJU’S – The Learning App today!