Surface area of a cone is the total area covered by its surface. The total surface area will cover the base area and lateral surface area of the cone. Cone is defined as a three-dimensional solid structure that has a circular base. A cone can be viewed as a set of non-congruent circular disks that are placed over one another such that the ratio of the radius of adjacent disks remains constant. In this article, let us discuss the formula for the surface area of a cone, its derivation with many solved examples.

What is Surface area of a Cone?

Surface area of a cone is the complete area covered by its two surfaces, i.e., circular base area and lateral (curved) surface area. The circular base area can be calculated using area of circle formula. The lateral surface area is the side-area of the cone. Let us see the formula to calculate the surface area of cone.

Surface Area of a cone Formula

The surface area of a cone is the total area occupied by its surface in a 3D plane. The total surface area will be equal to the sum of its curved surface area and circular base area.

Derivation of the Surface area of cone

Consider a cone as a triangle that is being rotated about one of its vertices. Now, think of a scenario where we need to paint the faces of a conical flask. Before painting, we need to know the quantity that is required to paint all the walls. We need to know the area of every face of the container to determine the quantity of paint required and this is known as the total surface area. The total surface area of a cone is the sum of areas of its faces. Let’s derive a general Cone formula to calculate the surface area of a cone.

Take a paper cone and cut it along its slant height to observe the figure being formed by the surface of the cone. Mark the two endpoints as A and B and the point of the intersection of lines as O.

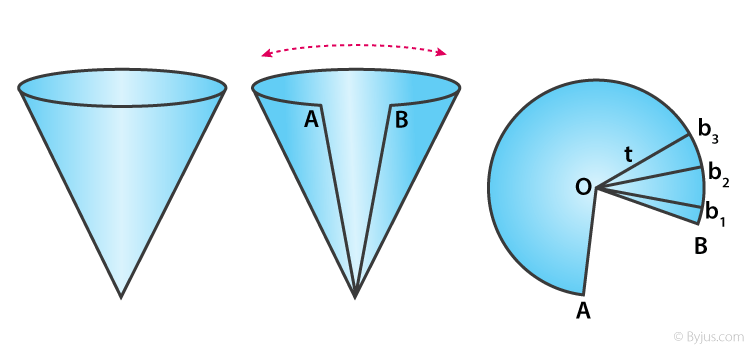
If you further cut this figure into multiple pieces’ viz. Ob₁, Ob₂, Ob₃, …….., Ob_n each measuring the same length as the slant height of the original cone, you will observe n triangles are formed out of it.

Now, if you try calculating the total area of this figure, you just need to add an area of these individual triangles. Hence,

Area of figure = (1/2) × (b₁ + b₂ + b₃ + ………….. + b_n)

=  (1/2)× (length of an entire curved boundary)

Length of entire curved boundary = circumference of base = 2π× r (where r is the radius of the base)

Thus, area of figure =  \(\frac{1}{2} \times 2 \pi \times r \times l= \pi rl\)

Hence, curved surface area of a cone = \(\pi rl\)

Total Surface Area of a Cone:

The Total surface area of a cone includes the curved surface as well as area of its base, which is given as-

Base Area = \(\pi r^{2}\)

Curved Surface Area = \(\pi rl\)

Thus the total surface area is given by-

\(\pi r^{2} + \pi r l = \pi r (r+ l)\)

Surface area of Right Circular Cone

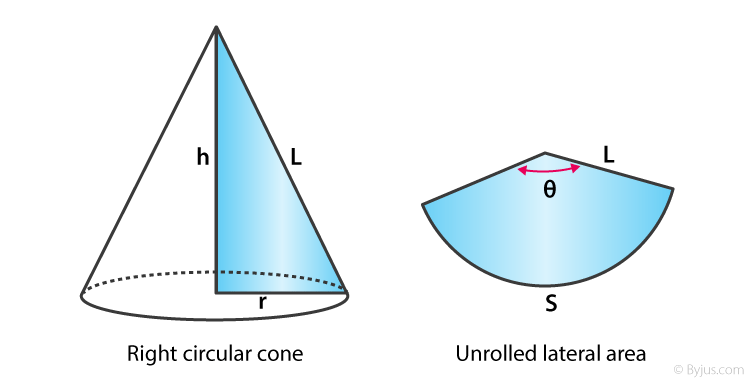
A circular cone is the one with the circular right section. A right circular cone is a circular cone whose axis is perpendicular to the base.

Surface area of cone = πr(r+√(h²+r²))
where r is the radius of the circular base
h is the height of the cone

Slant height of the cone, L = √(h²+r²)

Therefore,

Surface area = πr (r + L)

Curved Surface Area of a Cone

The curved surface of a cone is the area of the cone excluding the base. In other words, it is the area of the cone when it is unfolded as shown in the above figure as an unrolled lateral area. The formula to calculate the curved surface area of a cone is given by:

Curved Surface Area (CSA) = πrl

Here,

r = Radius of the circular base of the cone

l = Slant height of the cone

When the cone is in the form of an unrolled lateral area, r is referred to as the length of the arc of a sector and l is referred to as the radius of the sector.

Total Surface Area of a Cone

The total surface area of a cone is defined as the total area of the cone occupied in a three-dimensional area. It is equal to the sum of the curved surface and the base of the cone. The formula to calculate the total surface area of a cone is given by:

Total Surface Area (TSA) = CSA + Area of Circular Base

TSA = πr(r + l)

Slant Height of Cone

The slant height of the cone is the distance from the vertex to the edge of the circular base of the cone. The vertical height is the distance from the vertex to the center of circular base of cone.  The formula to find slant height of cone is given by:

Slant height of the cone, L = √(h²+r²)

where ‘h’ is the vertical height and ‘r’ is the radius of circular base of cone.

Related Articles

• Frustum Of A Cone
• Right Circular Cone
• Volume of a Cone

Solved Examples

Q.1. Determine the curved surface area of a cone whose base radius is 7 cm and slant height is 15 cm.

Solution: Curved surface area of a cone = πrl

= (22/7)× 7 ×15

=  330 cm²

Q.2. Calculate the Total surface area of a cone whose radius is 8 cm and height is 12 cm.

Solution- We know that the total surface area is given as

\( \pi r (r+ l)\)

Also, \(l = \sqrt{h^{2}+ r^{2}}\)

Also, \(l = \sqrt{8^{2}+ 12^{2}} = \sqrt{208} = 14.42\)

Thus Total Surface Area \(= \pi (8) (8 + 14.42)\)

\(= \pi (8) (22.42)\)

\(= 179.36 \pi\)