Tan 60 Degrees
The value of tan 60 degrees is √3. The word “Trigonometry” means measuring the sides of a triangle. An angle is a measure which is the amount of rotation of a revolving line with respect to the fixed-line. An angle is positive if the rotation is in an anti-clockwise direction and if the rotation is in a clockwise direction, then the angle is negative. The two types of conventions for measuring angles are
- Sexagesimal system
- Circular system.
In the sexagesimal system, consider a unit circle where the unit of measurement is the degree and it is denoted by the symbol ‘1°’. Each 1° is divided into 600 minutes (also denoted as 60’) and each minute is subdivided into 60 seconds and it is denoted by 60”.
Trigonometric ratios are represented for the acute angle as the ratio of the sides of a right angle triangle.
Tan 60 Degrees Value
In a right-angled triangle, the side opposite the right angle is called the hypotenuse side, the side opposite the angle of interest is called the opposite side and the remaining side is called the adjacent side where it forms a side of both the angle of interest and the right angle.
The tan function of an angle is equal to the length of the opposite side divided by the length of the adjacent side.
Tan θ = opposite side/ Adjacent Side
In terms of sine and cosine function, the tangent function is represented by
Tan θ = sin θ / Cos θ
Derivation to Find the Value of Tan 60 Degrees
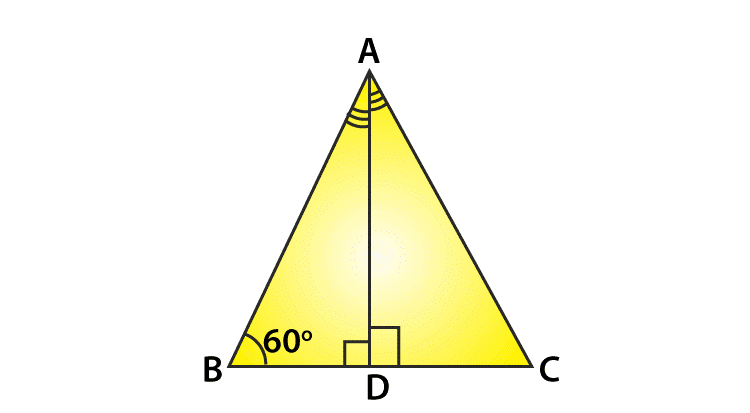
Tan 60 Degrees Value and Derivation
To find the value of tan 60 degrees geometrically, consider an equilateral triangle ABC since each of an angle in an equilateral triangle is 600.
Therefore, ∠A = ∠B = ∠C = 60°
Draw a perpendicular line AD from A to BC.
Now consider the triangle, ABD and ADC,
We have, ∠ ADB = ∠ADC= 90° and
∠ ABD = ∠ACD= 60°
Therefore, AD=AD
According to AAS Congruency,
Δ ABD ≅ Δ ACD
From this, we can say
BD = DC
Let us take, AB = BC =2a
Then, BD= ½ (BC) =½ (2a) =a
By using Pythagoras theorem,
AB2 = AD2– BD2
AD2= AB2-BD2
AD2 =(2a)2 – a2
AD2 = 4a2-a2
AD2 = 3a2
Therefore, AD=a√3
Now in triangle ADB,
Tan 600= AD/BD
= a√3/a = √3
Therefore, tan 60 degrees exact value is given by,
Tan 600=√3
In the same way, we can derive other values of tan degrees like 0°, 30°, 45°, 90°, 180°, 270° and 360°. Below is the trigonometry table, which defines all the values of tan along with other trigonometric ratios. We can easily learn the values of other tangent degrees with the help of sine functions and cosine functions. Just knowing the value of sine functions, we will find the values of cos and tan functions. There is an easy way to remember the values of tangent functions.
Sin 0° = √(0/4)
Sin 30° = √(1/4)
Sin 45° = √(2/4)
Sin 60° = √(3/4)
Sin 90° = √(4/4)
Now simplify all the sine values obtained and put in the tabular form:
| Angles (in degrees) | 0° | 30° | 45° | 60° | 90° |
| Sin | 0 | ½ | 1/√2 | √3/2 | 1 |
Now find the cosine function values. It is done as follows:
Cos 0° = Sin 90°
Cos 30° = Sin 60°
Cos 45° = sin 45°
Cos 60° = sin 30°
Cos 90° = sin 0°
| 0° | 30° | 45° | 60° | 90° | |
| Sin | 0 | ½ | √1/√2 | √3/2 | 1 |
| Cos | 1 | √3/2 | 1/√2 | 1/2 | 0 |
Since the tangent function is the function of sine and cosine function, find the values of tan can be obtained by dividing sin function by cos functions with respective degree values
So the tabular column that represents the tan function as
| 0° | 30° | 45° | 60° | 90° | |
| Sin | 0 | 1/2 | 1/√2 | √3/2 | 1 |
| Cos | 1 | √3/2 | 1/√2 | 1/2 | 0 |
| tan | 0 | 1/√3 | 1 | √3 | Not Defined |
Example: Calculate the value tan 9° – tan 27°- tan 63° + tan 81°
Solution:
Given, tan 9° – tan 27°- tan 63° + tan 81°
= tan 9° + tan 81° -tan 27°- tan 63°
= tan 9° + tan (90°-9°) – tan 27° – tan (90°- 27°)
= tan 9° + cot 9° -(tan 27°+ cot 27°) ……(1)
We can write,
tan 9°+ cot 9° = 1/ sin 9°cos 9°
= 2/ sin 18° ……………(2)
tan 27° + cot 27° = 1/ sin 27° cos 27°
= 2/ sin 54°
= 2/ cos 36° ………..(3)
Substitute (2) and (3) in (1), we get
tan 9° + cot 9° -(tan 27°+ cot 27°) = (2/ sin 18° )- (2/ cos 36°)
= 4
Therefore, the value of tan 9° – tan 27°- tan 63° + tan 81° = 4
Keep visiting BYJU’S for more information on trigonometric ratios and its related articles, and also watch the videos to clarify the doubts.
Learn More: