Vector Algebra For Class 12
Vector Algebra for class 12 is all about the study of vectors and scalars. There are various quantities, which involves magnitude as well as direction. If the quantity that has magnitude, as well as direction, is known as vectors. Such quantities are known as Vector Quantities. Eg: Displacement, velocity, acceleration, force, weight, momentum, electric intensity etc. Check here: Magnitude of a Vector.
Class 12 Vector Algebra Concepts
The concept of vectors is used to describe the physical quantities having directions and magnitude associated with them. A scalar is a physical quantity which is completely described by a constant or a single value. Class 12 Vector algebra NCERT Maths chapter 10 includes various important concepts from this topic like vector types, operations, etc. In this lesson, the key points that are covered from this class 12 Maths vector algebra chapter include vector introduction, types of vectors, and operations on vectors like addition. The topics and sub-topics covered in class 12 are:
- Introduction
- Some Basic Concepts
- Types of Vectors
- Addition of Vectors
- Multiplication of a Vector by a Scalar
- Product of Two Vectors
- Scalar (or dot) product of two vectors
- Projection of a vector on a line
- Vector (or cross) product of two vectors
Vector Algebra for Class 12 Notes
In vector algebra for class 12, some basic concepts of vectors like position vectors and the relationship between magnitude, direction ratios and direction cosines are explained in detail.
Position Vector
The position vector is given with respect to the origin O (0,0,0), where the coordinate of point (say P) is P(x,y,z) is given as-
\(\overline{OP} = \sqrt{x^{2} + y^{2} + z^{2}}\)Relationship Between Magnitude, Direction Ratios and direction cosines
The magnitude (r), direction ratios (a, b, c) and direction cosines (l, m, n) of any vector are related as l=(a/r), m=(b/r) n=(c/r)
Types of Vectors
The various types of vectors included in vector algebra for class 12 concepts are
(i) Zero Vector
(ii) Unit Vector
(iii) Co-initial Vectors
(iv) Collinear Vectors
(v) Equal Vectors
(vi) Negative of a Vector
Operations on Vectors
Vector Algebra includes addition, subtraction, and three types of multiplication between vectors. Below we will see how to perform addition on two vectors.
Addition of Vectors
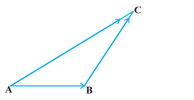
Consider a vector AB and vector BC, where the starting of sector vector is same as the end of the first vector, then the sum of two vectors is represented by a vector joining two vectors AC.
\(\overline{AC} = \overline{AB} + \overline{BC}\)This is known as the triangle law of vector addition and is essentially used to find the geometrical sum of two or more vectors.
Read More on other Vectors Operations
Vector Algebra For Class 12 Examples

Keep visiting BYJU’S for additional maths notes for all the classes. Also, get various video lessons on different topics to learn in a more engaging and effective way by registering at BYJU’S and downloading the app now.