Volume of a Prism
A prism is a polyhedron in which all the faces are flat, and the bases are parallel to each other. It is a solid object with flat faces, identical ends, and the same cross-section along with its length. In Geometry, we will learn the different types of prisms, such as a triangular prism, pentagonal prism, and hexagonal prism. Since it is a three-dimensional shape, a prism has a surface area and volume. In this article, we are going to discuss the volume of a prism, its formulas and solved problems.
| Also, read: |
What is the Volume of a Prism?
The volume of a prism is defined as the total space occupied by the three-dimensional object. Mathematically, it is defined as the product of the area of the base and the length.
Therefore,
The volume of a Prism = Base Area × Length
The measurement unit used to represent the volume of a three-dimensional object is cubic units.
Volume of a Prism Formula
Now, let us discuss the volume of the different prism formulas such as the volume of the triangular prism, rectangular prism, pentagonal prism, and so on.
Volume of a Triangular Prism
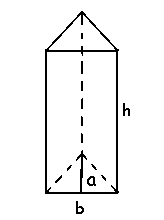
A triangular prism is a prism that has three rectangular faces and two triangular bases. Since the cross-section of the triangular prism is a triangle, the formula for the volume of a triangular prism is given as:
The volume of a Triangular Prism = (½) abh cubic units.
Where
a = Apothem length of a triangular prism
b = Base length of a triangular prism
h = height of a triangular prism
Volume of a Rectangular prism
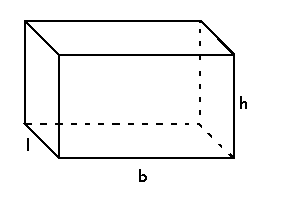
A rectangular prism has four rectangular faces and two parallel rectangular bases. We know that the cross-section of a rectangular prism is a rectangle. The rectangular prism is also known as “Cuboid”.
Hence, the formula to find the volume of a rectangular prism is given as:
The volume of a Rectangular Prism = lbh cubic units.
Where
l = Base width of a rectangular prism
b = Base length of a rectangular prism
h = height of a rectangular prism
Volume of a Pentagonal Prism
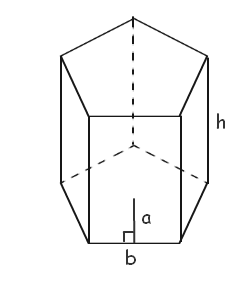
A pentagonal prism has five rectangular faces and two parallel pentagonal bases. Since the base area of the pentagonal prism is (5/2) ab, the volume of the pentagonal prism is given as:
The Volume of a Pentagonal Prism = (5/2) abh cubic units
Where,
a – Apothem length of the pentagonal prism.
b – Base length of the pentagonal prism.
h – Height of the pentagonal prism
Volume of a Hexagonal Prism
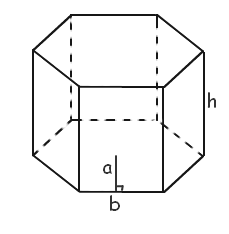
A hexagonal prism is a prism with six rectangular faces and two parallel hexagonal bases. The base area of the hexagonal prism is 3ab, the formula to find the volume of a hexagonal prism is given as:
The volume of a Hexagonal Prism = 3abh cubic units
Where
a – Apothem length of the hexagonal prism.
b – Base length of the hexagonal prism.
h – Height of the hexagonal prism.
Volume of a Prism Example
Question 1:
What is the volume of a triangular prism with dimensions 12 m, 16 m and 20 m as given in figure.
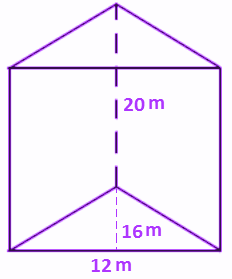
Solution:
volume of a triangular prism can be found by V = Area of base × Height of Prism
As the base is triangular, So , Area of triangle = ½ × base × height = ½ × base × height =½ × 12 × 16 = 96
So, Volume of prism = 96 × 20 = 1920 cubic meter
To learn more formulas, register with BYJU’S – The Learning App and download the app to practice more problems.