What is a Plane?
A plane, in geometry, prolongs infinitely in two dimensions. It has no width. We can see an example of a plane in coordinate geometry. The coordinates define the position of points in a plane.
In Maths, a plane is a flat, two-dimensional surface that prolongs infinitely far. A plane is a two-dimensional analogue that could consist of a point, a line and three-dimensional space. Planes can appear as subspaces of a few higher-dimensional spaces, like the room’s walls extended exceptionally far away. These walls experience an independent existence on their own, as in the framework of Euclidean geometry.
What is a point?
A point is a location in a plane that has no size, i.e. no width, no length and no depth.
What is a line?
A line is a set of points that stretches infinitely in opposite directions. It has only one dimension, i.e., length. The points that lie on the same line are called collinear points.
Plane in Algebra
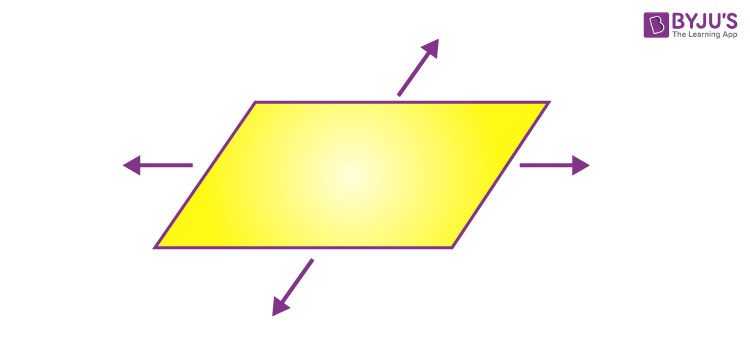
In algebra, the points are plotted in the coordinate plane, and this denotes an example of a geometric plane. The coordinate plane has a number line, extending left to right endlessly and another one extending up and down infinitely. It is impossible to view the complete coordinate plane.
Arrows designate the truth that it extends infinitely along the x-axis and the y-axis on the number lines’ ends. These number lines are two-dimensional, where the plane extends endlessly. When we plot the graph in a plane, then the point or a line, plotted does not have any thickness.
Also, learn:
Plane Meaning
A surface comprising all the straight lines that join any two points lying on it is called a plane in geometry. In other words, it is a flat or level surface. In a Euclidean space of any number of dimensions, a plane is defined through any of the following uniquely:
Using three non-collinear points
Using a point and a line not on that line
Using two distinct intersecting lines
Using two separate parallel lines
Intersecting Planes
Two planes can be related in three ways, in a three-dimensional space.
They can be parallel to each other
They can be identical
They can intersect each other
The figure below depicts two intersecting planes.
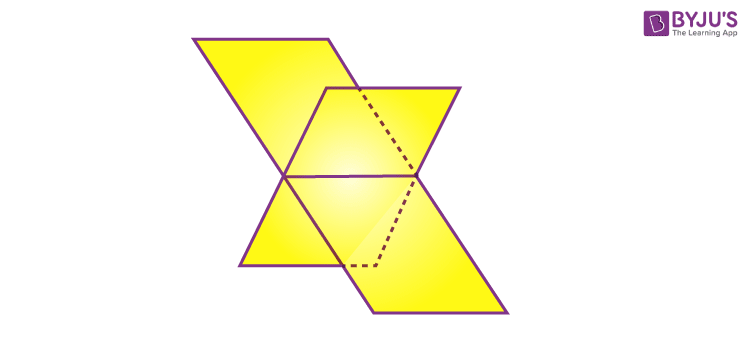
The method to get the equation of the line of intersection connecting two planes is to determine the set of points that satisfy both the planes’ equations. Since the equation of a plane comprises three variables and two equations (because of two planes), solving the simultaneous equations will give a relationship between the three variables, which is equal to the intersection line equation.
Properties of a Plane
If there are two different planes than they are either parallel to each other or intersecting in a line, in a three-dimensional space
A line could be parallel to a plane, intersects the plane at a single point or is existing in the plane.
If there are two different lines, which are perpendicular to the same plane then they must be parallel to each other.
If there are two separate planes that are perpendicular to the same line then they must be parallel to each other.
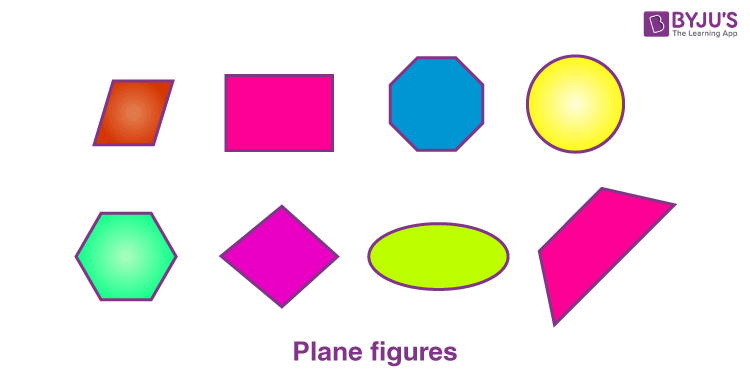
What is a Plane Figure?
A plane figure is defined as a geometric figure that has no thickness. It lies entirely in one plane. It is possible to form a plane figure c with line segments, curves, or a combination of these two, i.e. line segments and curves. Let’s have a look at some examples of plane figures in geometry such as circle, rectangle, triangle, square and so on. These are given in the below figure.