Area of Ellipse
Definition
An ellipse is a curve on a plane such that the sum of the distances to its two focal points is always a constant quantity from any chosen point on that curve. The ellipse belongs to the family of circles with both the focal points at the same location. In an ellipse, if you make the minor and major axis of the same length with both foci F1 and F2 at the center, then it results in a circle.
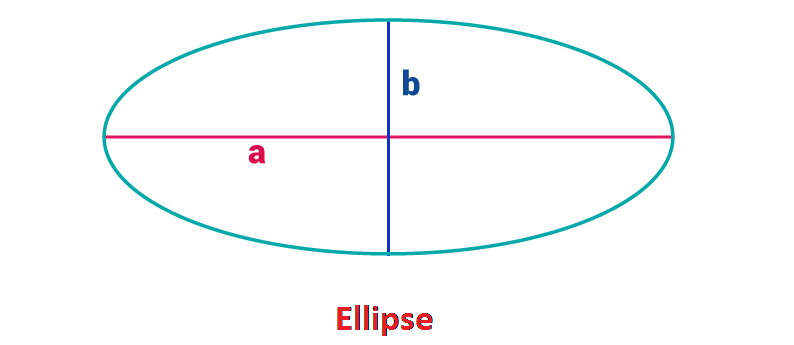
Area of an Ellipse
Area= π ab
Where a and b denote the semi-major and semi-minor axes respectively.
The above formula for area of the ellipse has been mathematically proven as shown below:
We know that the standard form of an ellipse is:
For Horizontal Major Axis
x2 /a2 + y2 /b2 = 1, (where a>b)
Or, \(y = b.\sqrt{1-\left ( \frac{x}{a} \right )^{2}}\)
For Vertical Major Axis
x2 /b2 +y2 /a2 = 1, (where a>b)
Or, \(y = a.\sqrt{1-\left ( \frac{x}{b} \right )^{2}}\)
Area of an Ellipse Proof
We know the general equation for an ellipse is \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}} = 1\) \(y = b.\sqrt{1-\left ( \frac{x}{a} \right )^{2}}\) \(y = \frac{b}{a}\sqrt{a^{2} – x^{2}}\) As we can see the ellipse is divided into four quadrants. So calculating the area of 1 quadrant and multiplying by 4, we get the area of an ellipse. Area, \(A = 4. \int_{0}^{a} y.dx\) \(A = 4. \int_{0}^{a} \frac{b}{a} \sqrt{a^{2}-x^{2}} dx\) \(= 4. \frac{b}{a}\int_{0}^{a} \sqrt{a^{2}-x^{2}} dx\) Substituting x = a sin t dx = a cos t . dt x = 0 changes to t = 0 and x = a changes to t = π/2 \(A = 4. \frac{b}{a}\int_{0}^{\frac{\pi}{2}} \sqrt{a^{2}-a^{2} \sin^{2}t} .a \cos t .dt\) Now, cancel out the term “a”, we get \(A = 4b \int_{0}^{\pi/2}\sqrt{a^{2}(1-sin^{2}t)} cost dt\)\(A = 4ba \int_{0}^{\pi/2}\sqrt{cos^{2}t} cost dt\) \(A = 4ba \int_{0}^{\pi/2}cos^{2}t dt\) \(A = 4ab \left ( \frac{t}{2} + \frac{\sin 2x}{4} \right )_{0}^{\pi/2}\) \(A = 4ab (\frac{\pi}{4})\) \(A = \pi ab\) |
Applications of Ellipse
They have wide applications in the field of Engineering, Physics, etc. For instance, all the planets revolve in their orbits which are elliptical. Moreover, astronomy has a lot of use of this shape as many of the stars and planets are shaped as ellipsoids.
This is all about the area of an ellipse. To know more about the various attributes of the ellipse and other geometrical figures, please do visit www.byjus.com or download BYJU’S-The Learning App.