Arithmetic Mean And Range
In statistics, the Arithmetic Mean (AM) or called average is the ratio of the sum of all observations to the total number of observations. The arithmetic mean can also inform or model concepts outside of statistics. In a physical sense, the arithmetic mean can be thought of as a centre of gravity. From the mean of a data set, we can think of the average distance the data points are from the mean as standard deviation. The square of standard deviation (i.e. variance) is analogous to the moment of inertia in the physical model.
Say, for example, you wanted to know the weather in Shimla. On the internet, you would find the temperatures for a lot of days, data of the temperature in the past and the data of the temperature in the present and also the predictions of the temperature in the future. Wouldn’t all this be extremely confusing? Instead of this long list of data, mathematicians decided to use representative values that could take into consideration a wide range of data. Instead of weather for every particular day, we use terms such as average (arithmetic mean), median and mode to describe weather over a month or so. There are several types of representative values that are used by Mathematicians in data handling, namely;
- Arithmetic Mean (Average)
- Range
- Median
- Mode
Out of the four above, mean, median and mode are types of average
Read: Mean, Median and Mode
What is Arithmetic Mean?
Arithmetic mean represents a number that is obtained by dividing the sum of the elements of a set by the number of values in the set. So you can use the layman term Average, or be a little bit fancier and use the word “Arithmetic mean” your call, take your pick -they both mean the same. The arithmetic mean may be either
- Simple Arithmetic Mean
- Weighted Arithmetic Mean
Arithmetic Mean Formula
If any data set consisting of the values b1, b2, b3, …., bn then the arithmetic mean B is defined as:
B = (Sum of all observations)/ (Total number of observation)
= 1/n \(\sum_{i=1}^n b_i = \frac{b_1+b_2+b_3+….+b_n}{n}\)
If these n observations have corresponding frequencies, the arithmetic mean is computed using the formula
x = \(\frac{x_{1}f_{1}+x_{2}f_{2}+……+x_{n}f_{n}}{N}\) and
using Sigma notation = \(\frac{\sum_{i=1}^{n}x_{i}f_{i}}{N}\)
where N = f1+ f2 + ……….+ fn.
The above formula can also be used to find the weighted arithmetic mean by taking f1, f2,…., fn as the weights of x1, x2,….., xn.
When the frequencies divided by N are replaced by probabilities p1, p2, ……,pn we get the formula for the expected value of a discrete random variable.
X = x1p1 + x2p2 +…….+ xnpn. or
using Sigma notation = \(\sum_{i=1}^{n}x_{i}p_{i}\)
Properties of Arithmetic Mean
Some important properties of the arithmetic mean are as follows:
- The sum of deviations of the items from their arithmetic mean is always zero, i.e. ∑(x – X) = 0.
- The sum of the squared deviations of the items from Arithmetic Mean (A.M) is minimum, which is less than the sum of the squared deviations of the items from any other values.
- If each item in the arithmetic series is substituted by the mean, then the sum of these replacements will be equal to the sum of the specific items.
Arithmetic Mean of Ungrouped Data
For ungrouped data, we can easily find the arithmetic mean by adding all the given values in a data set and dividing it by a number of values.
Mean, x̄ = Sum of all values/Number of values
Example: Find the arithmetic mean of 4, 8, 12, 16, 20.
Solution: Given, 4, 8, 12, 16, 20 is the set of values.
Sum of values = 4+ 8+12+16+20 = 60
Number of values = 5
Mean = 60/5 = 12
Arithmetic Mean of Ungroued Data
If x1, x2, x3 ,……,xn be the observations with the frequencies f1, f2, f3 ,……,fn, then the arithmetic mean is given by:
x̄ = (x1f1+x2f2+……+xnfn) / ∑fi
where ∑fi is the summation of all the frequencies.
Let us understand the arithmetic mean of ungrouped data with the help of an example.
Example: Find the mean of given distribution:
| x | 10 | 20 | 30 | 40 | 50 |
| f | 3 | 2 | 4 | 5 | 1 |
Solution: Let us find the value of xifi and ∑fi, for all the values of x and f respectively.
| xi | fi | xifi |
| 10 | 3 | 10 x 3 = 30 |
| 20 | 2 | 20 x 2 = 40 |
| 30 | 4 | 30 x 4 = 120 |
| 40 | 5 | 40 x 5 = 200 |
| 50 | 1 | 50 x 1 = 50 |
| Total | ∑fi = 15 | ∑xifi = 440 |
Hence, the required mean is:
x̄ = 440/15 = 29.33
Merits of Arithmetic Mean
-
The arithmetic mean is simple to understand and easy to calculate.
-
It is influenced by the value of every item in the series.
-
A.M is rigidly defined.
-
It has the capability of further algebraic treatment.
-
It is a measured value and not based on the position in the series.
Demerits of Arithmetic Mean
-
It is changed by extreme items such as very small and very large items.
-
It can rarely be identified by inspection.
-
In some cases, A.M. does not represent the original item. For example, the average number of patients admitted to a hospital are 10.7 per day.
-
The arithmetic mean is not suitable in extremely asymmetrical distributions.
Representative Values of Data
We see the use of representative value quite regularly in our daily life. When you ask about the mileage of the car, you are asking for the representative value of the amount of distance travelled to the amount of fuel consumed. This doesn’t mean that the temperature in Shimla in constantly the representative value but that overall, it amounts to the average value. Average here represents a number that expresses a central or typical value in a set of data, calculated by the sum of values divided by the number of values.
Arithmetic Mean Example
Arithmetic means utilizes two basic mathematical operations, addition and division to find a central value for a set of values.
Example: If you wanted to find the arithmetic means of the runs scored by Virat Kohli in the last few innings, all you would have to do is sum up his runs to obtain sum total and then divide it by the number of innings. For example;
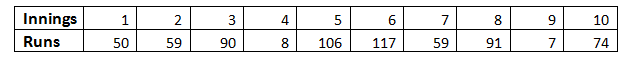
The arithmetic mean of Virat Kohli’s batting scores also called his Batting Average is;
Sum of runs scored/Number of innings = 661/10
The arithmetic mean of his scores in the last 10 innings is 66.1. If we add another score to this sum, say his 11th innings, the arithmetic mean will proportionally change. If the runs scored in 11th innings are 70, the new average becomes;
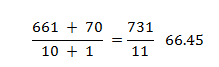
The average is a pretty neat tool, but it comes with its set of problems. Sometimes it doesn’t represent the situation accurately enough. I’ll show you what I mean. Let’s take the results of a class test, for example. Say there are 10 students in the class and they recently gave a test out of 100 marks. There are two scenarios here.
First: 50, 53, 50, 51, 48, 93, 90, 92, 91, 90
Second: 71, 72, 70, 75, 73, 74, 75, 70, 74, 72
Why don’t you calculate the Arithmetic mean of both the sets above? You will find that both the sets have a huge difference in the value even though they have similar arithmetic mean. In this respect, completely relying on arithmetic mean can be occasionally misleading. At least from the point of view of students scoring 50’s/ 100, the second scenario is quite different. The same applies to the students with 90, in the case of these students in the second set, the marks are reduced. So for both the classes, the results mean something different, but the average for both classes are the same. In the first class, the students are performing very varied, some very well and some not so well whereas in the other class the performance is kind of uniform. Therefore we need an extra representative value to help reduce this ambiguity.
Arithmetic Range
Range, as the word suggests, represents the difference between the largest and the smallest value of data. This helps us determine the range over which the data is spread—taking the previous example into consideration once again. There are 10 students in the class, and they recently gave a test out of 100 marks. There are two scenarios here.
First: 50, 53, 50, 51, 48, 93, 90, 92, 91, 90
Second: 71, 72, 70, 75, 73, 74, 75, 70, 74, 72
The range in the first scenario is represented by the difference between the largest value, 93 and the smallest value, 48.
Range in First set = 93 – 48 = 45
Whereas in the second scenario, the range is represented by the difference between the highest value, 75 and the smallest value, 70.
Range in the second set = 75 – 70 = 5
The difference in the value of range between the two scenarios enables us to estimate the range over which the values are spread, the larger the range, the larger apart the values are spread. This gives us the extra information which is not getting through on average.
Related Articles
- Central Tendency
- Average
- Arithmetic Mean Statistics
- Arithmetic Mean and Range
- Mean Deviation For Ungrouped Data
- Difference Between Average and Mean
Frequently Asked Questions on Arithmetic Mean
What is meant by the arithmetic mean?
The arithmetic mean or mean is the simplest way to calculate the average for the given set of numbers. It is classified into two different types, namely simple arithmetic mean and weighted arithmetic mean.
How to calculate the arithmetic mean?
The arithmetic mean is defined as the ratio of the sum of all the given observations to the total number of observations. For example, if the data set consists of 5 observations, the arithmetic mean can be calculated by adding all the 5 given observations divided by 5.
How to find the arithmetic mean between 2 numbers?
Add the two given numbers and then divide the sum by 2. For example, 2 and 6 are the two numbers, the arithmetic mean is calculated as follows:
Arithmetic Mean = (2+6)/2 = 8/2 = 4
Why is arithmetic mean considered to be the best measure of central tendency?
To calculate the central tendency for the given data set, we use different measures like mean, median, mode and so on. Among all these measures, the arithmetic mean or mean is considered to be the best measure, because it includes all the values of the data set. If any value changes in the data set, this will affect the mean value, but it will not be in the case of median or mode.
Can arithmetic mean be negative?
Yes, the arithmetic mean can be negative. The data can be distributed anywhere. So, the mean value can be negative or positive or zero.
Learn more about the fascinating world of Mathematics by downloading BYJU’S – The Learning App. Join us and fall in love with learning.