Concurrent Lines
Concurrent lines are the lines, in 2-D geometry, which intersect each other exactly at one point. The meaning of concurrent is happening at the same time or point. The intersecting lines are always concurrent.
Concurrent lines are non-parallel lines and extend indefinitely at both the direction. They intersect each other at a point somewhere in the plane. Thus we can say all parallel lines are not concurrent lines.
| Table of Contents: |
Definition
When two or more lines pass through a single point, in a plane, they are concurrent with each other and are called concurrent lines. A point that is common to all those lines is called the point of concurrency. This property of concurrency can also be seen in the case of triangles.
All the intersecting lines or non-parallel lines are concurrent. But parallel lines are not concurrent at any point on a plane.
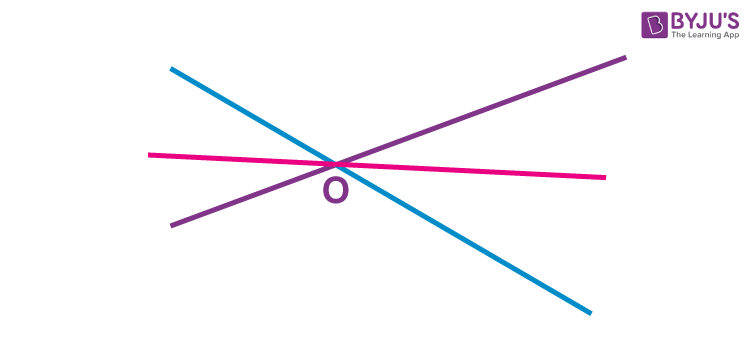
In the figure given below, you can see the three lines are all crossing point O. Hence, all these three lines are concurrent with each other.
Condition of Concurrent Lines
If three lines are concurrent, then the point of intersection of two lines lies on the third line. Suppose, the equations of three lines are:
a1 x + b1y + c1 = 0 ……………. (1)
a2 x + b2 y + c2 = 0 ……………. (2)
a3 x + b3 y + c3 = 0 ……………. (3)
Thus, the condition, if the three lines are concurrent to each other, is;
\(\left|\begin{array}{lll} a_{1} & b_{1} & c_{1} \\ a_{2} & b_{2} & c_{2} \\ a_{3} & b_{3} & c_{3} \end{array}\right|=0\)
Solved Example
Question: Find if the lines 2x – 3y + 5 = 0, 3x + 4y – 7 = 0 and 9x – 5y + 8 =0 are concurrent.
Answer: Given the three lines are:
2x – 3y + 5 = 0
3x + 4y – 7 = 0
9x – 5y + 8 =0
Now, as per the condition of the concurrence of lines, we need to find the determinant of the coefficients.
Hence,
\(\left|\begin{array}{lll} 2 & -3 & 5 \\ 3 & 4 & -7 \\ 9 & -5 & 8 \end{array}\right|=0\)
= 2(32 – 35) – (-3)(24 + 63) + 5(-15 – 36)
= 2(-3) + 3(87) + 5(-51)
= – 6 + 261 -255
= 0
Therefore, the given three lines are concurrent.
Concurrent Lines in Triangles
In a triangle, the concurrent lines are:
- Altitudes
- Medians
- Angle bisectors
- Perpendicular bisectors
| Altitudes | The three altitudes of triangle from all the three vertices intersects each other at a common point. This point where the altitudes intersect is called the orthocenter. |
| Medians | The three medians of triangle that divides the opposite side into equal parts and intersects at a single point, known as the centroid. |
| Angle Bisectors | Angle bisectors are the rays that bisect the angle from each vertex and meet at a single point. The point is called here as incenter. |
| Perpendicular Bisectors | The perpendicular bisectors are the lines that intersect the opposite sides at 90 degree angles and pass through a single point. This point is called the circumcenter. |
Concurrent Line Segments and Rays
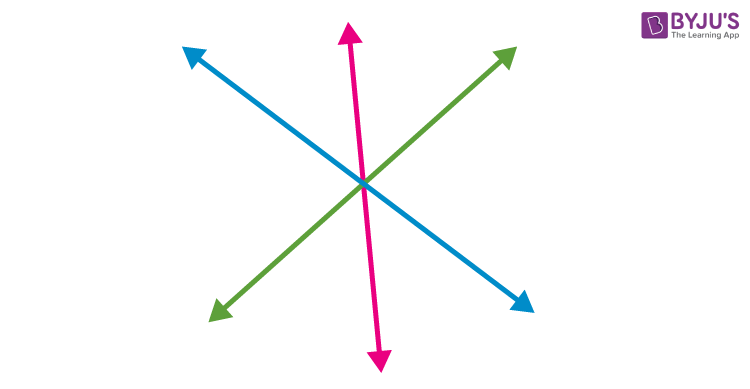
When three or more line segments, intersect each other at a single point, then they are said to be concurrent line segments. See the figure below, where AB, CD and EF are three line segments and are intersecting each other at one point O. Hence, we can apply the concurrency to line segments also.

When three or more Rays in 2-D plane cuts or meets at a single point, then they are called Concurrent Rays. The single point is the point of concurrency for all the rays. In the below figure, three rays PQ, RS and MN, which are intersecting at a point O, are concurrent to each other.
Difference Between Concurrent Lines and Intersecting Lines
As we have already understood, if any three lines or line segments or rays are having a single intersection point, they are said to be in concurrency. While, in the case of intersecting lines, there are only two lines or line segments or rays that intersect with each other. We can write the differences in a tabular form.
| Concurrent Lines | Intersecting LInes |
| Three or more lines pass through a single point. | Only two lines intersect each other |
| The single point at which these lines intersect each other is called a point of concurrency. | The point where two lines intersect is called the point of intersection. |
| Example:
|
Example:
|
Stay tuned with BYJU’S – The Learning App and also download the app for more interesting Maths-related concepts and personalized videos.
Related Articles
| Perpendicular Lines Geometry | Properties Of Parallel Lines |
| Coplanarity Two Lines | Distance Between Two Lines |