In Mathematics, we mostly prefer the distance formula to find the distance between the two points in the coordinate plane. This distance formula is used when we know the coordinates of the two points in the plane. In that case, by substituting those points in the formula, we can easily get the distance between two points. In order to locate the position of a point in a plane or two dimensions, we require a pair of the coordinate axis. The distance of the point along the x-axis from the centre is called x-coordinate (or abscissa), and the distance of the point along the y-axis from the origin is called y-coordinate (or ordinate). The ordered pair (x,y) represents the coordinate of the point. In this article, you will learn the distance between two points in the 2D  plane (two-dimensional plane)  and 3D plane (three-dimensional plane), formulas and examples in detail.

Distance Between 2 Points Formula

Consider two points \(A(x_{1},y_{1})\;and\;B(x_{2},y_{2})\) on the given coordinate axis. The distance between these points is given as:

\(d=\sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2}\)

Also try: Distance Between Two Points Calculator

How to Find the Distance Between Two Points?

To find the distance between two points in the coordinate plane, follow the procedure given below:

• To find the distance between two points, take the coordinates of two points such as (x₁, y₁) and (x₂, y₂)
• Use the distance formula (i.e) square root of  (x₂ – x₁)² + (y₂ – y₁)²
• For this formula, calculate the horizontal and vertical distance between two points. Here, the horizontal distance (i.e) (x₂ – x₁) represents the points in the x-axis, and the vertical distance (i.e) (y₂ – y₁) represents the points in the y-axis
• Square both the values such as the square of (x₂ – x₁) and the square of (y₂ – y₁)
• Add both the values (i.e) (x₂ – x₁)² + (y₂ – y₁)²
• Now, take the square root of the obtained value
• Thus, the final value gives the distance between two points in the coordinate plane

Distance Between Two Points in 3D

Distance Between 2 Points Formula in 3D

The distance between two points P(x₁, y₁, z₁) and Q(x₂, y₂, z₂) = PQ = √[(x₂ – x₁)² + (y₂ – y₁)² + (z₂ – z₁)²]

Distance Between 2 Points Formula Derivation in 3D

Let the points \(P(x_{1},y_{1},z_{1})\) and \(Q(x_{2},y_{2},z_{2})\) be referred to a system of rectangular axes OX,OY and OZ as shown in the figure.

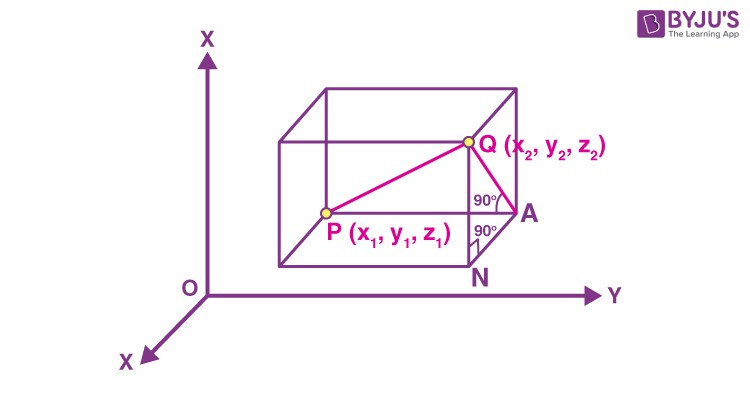
Through the points P and Q, we draw planes parallel to the rectangular coordinate plane such that we get a rectangular parallelepiped with PQ as the diagonal. ∠PAQ forms a right angle and therefore, using the Pythagoras theorem in triangle PAQ,

\(PQ^2= PA^2+AQ^2\)………(1)

Also, in triangle ANQ, ∠ANQ is a right angle. Similarly, applying the Pythagoras theorem in ΔANQ we get,

\(AQ^2=AN^2+NQ^2\)……..(2)

From equations 1 and 2 we have,

\(PQ^2=PA^2+NQ^2+AN^2\)

As coordinates of the points, P and Q are known,

\(PA=y_{2}-y_{1}\), \(AN=x_{2}-x_{1}\) and \(NQ=z_{2}-z_{1}\)

Therefore,

\(PQ^2=(x_2-x_1 )^2+(y_2-y_1 )^2+(z_2-z_1 )^2\)

Thus, the formula to find the distance between two points in three-dimension is given by:

\(PQ=\sqrt{(x_2-x_1 )^2+(y_2-y_1 )^2+(z_2-z_1 )^2}\)

This formula gives us the distance between two points \(P(x_1,y_1,z_1)\) and \(Q(x_2,y_2,z_2)\) in three dimensions.

Distance of any point \(Q(x,y,z)\) in space from origin \(O(0,0,0)\), is given by,

\(OQ=\sqrt{(x^2+y^2+z^2)}\)

Distance Between Two Points Examples

Let us go through some examples to understand the distance formula in three dimensions.

Example 1:

Find the distance between the two points given by P(6, 4, -3) and Q(2, -8, 3).

Solution:

Let the given points be:

P(6, 4, -3) = (x₁, y₁, z₁)

Q(2, -8, 3) = (x₂, y₂, z₂)

Using distance formula to find distance between the points P and Q,

\(PQ=\sqrt{((x_2-x_1 )^2+(y_2-y_1 )^2+(z_2-z_1 )^2 )}\)

\(PQ=\sqrt{(6-2)^2+(4-(-8))^2+(-3-3)^2}\)

\(PQ=\sqrt{(16+144+36)}\)

PQ = √196

PQ = 14

Example 2: A, B, C are three points lying on the axes x,y and z respectively, and their distances from the origin are given as respectively; then find coordinates of the point which is equidistant from A, B, C and O.

Solution:

Let the required point be P(x, y, z).

Co-ordinates of the points A,B and C are given as (a, 0, 0), (0, b, 0), (0, 0, c)  and (0, 0, 0).

As we know that the point P is equidistant from the given points.

Hence, PA = PB = PC = PO

Now, applying the distance formula for PO = PA, we get

\(\sqrt{x^2+y^2+z^2}=\sqrt{(a-x)^2+y^2+z^2}\)

\(x^2+y^2+z^2=(a-x)^2+y^2+z^2\)

\(x^2=(a-x)^2\)

\(x= a/2\)

Similarly applying the distance formula for PO = PB and PO=PC, we get \(y= \frac{b}{2}\) and \(z= \frac{c}{2}\).

Therefore co-ordinates of the point  which are equidistant from the points A,B,C and O is given by\((\frac{a}{2},\;\frac{b}{2},\;\frac{c}{2})\).

Example 3: 

Find the distance between two points A(7, 13) and B(10, 9).

Solution:

Given:

Two points are A(7, 13) = (x₁, y₁) and B(10, 9) = (x₂, y₂).

We know that the formula to calculate the distance between two points is:

AB = √[(x₂-x₁)² + (y₂-y₁)²]

Now, substitute the values in the formula, we get

AB = √[(10-7)² + (9-13)²]

AB = √[(3)²+ (-4)²]

AB = √(9+16) = √25 

AB = 5

Hence, the distance between two points A(7, 13) and B(10, 9) is 5.

Example 4:

The distance between two points (a, 2) and (3, 4) is 8. Find the value of a.

Solution:

Let the points be P and Q.

(i.e) P ( a, 2) = (x₁, y₁) and Q(3, 4) = (x₂, y₂)

We know that the distance between two points formula is:

PQ = √[(x₂-x₁)² + (y₂-y₁)²]

Now, substitute the values, we get

8 = √[(3-a)² + (4-2)²]

Now, take square on both sides, we get

8² = (3-a)² + (4-2)²

64 = (3-a)²+ 2²

64 = (3-a)² +4

(3-a)² = 60

Now, take square root on both sides, we get

3-a = √60

3-a = ±2√15

Hence, a = 3±2√15.

Therefore, the value of a is 3±2√15.

Example 5: 

Determine the distance between two points (7, 5) and (3, 2)

Solution:

(7, 5) = (x₁, y₁)

(3, 2) = (x₂, y₂)

We know that, the distance between two points formula is:

Distance = √[(x₂-x₁)² + (y₂-y₁)²]

Distance = √[(3-7)² + (2-5)²]

Distance =√[(-4)²+ (-3)²] = √(16+9) = √25

Distance = 5 units.

Therefore, the distance between the two points is 5 units.

Practice Problems

1. Show that the points P (–2, 3, 5), Q (1, 2, 3) and R (7, 0, –1) are collinear using the distance formula.
2. What is the distance between two points (3, 4, 5) and (–1, 3, –7)?
3. Verify that (0, 7, –10), (1, 6, – 6) and (4, 9, – 6) are the vertices of an isosceles triangle.

To learn more about three-dimensional geometry, please visit our website www.byjus.com or download BYJU’S- The Learning App.