Finding The Perfect Cube of Numbers
A perfect cube of a number is a number that is equal to the number, multiplied by itself, three times. If x is a perfect cube of y, then x = y3. Therefore, if we take the cube root of a perfect cube, we get a natural number and not a fraction. Hence, 3√x = y. For example, 8 is a perfect cube because 3√8 = 2. The major application of cubes can be seen in geometry while determining the volume of a cube (a 3d shape). Let us learn here the definition, list of perfect cubes, applications with examples.
What are Perfect Cubes?
Perfect cubes are the numbers that are the triple product of the same number. In other words, a perfect cube is a value that is the result of three times multiplication of a whole number to itself. A perfect cube is a number, that can be written as three times the product of the same number.
The cube root of a perfect cube always results in a whole number. But we can find cubes of any number whether it is an integer or a fraction. For example, the cube of 0.5 is:
0.5 × 0.5 × 0.5 = 0.125
Let us see the list of perfect cubes in the next section.
List of Perfect Cubes 1 to 50
| Number (x) | Multiplied Three times by itself | Cubes (x3) |
| 1 | 1× 1× 1 | 1 |
| 2 | 2× 2× 2 | 8 |
| 3 | 3× 3× 3 | 27 |
| 4 | 4× 4× 4 | 64 |
| 5 | 5× 5× 5 | 125 |
| 6 | 6× 6× 6 | 216 |
| 7 | 7× 7× 7 | 343 |
| 8 | 8× 8× 8 | 512 |
| 9 | 9× 9× 9 | 729 |
| 10 | 10× 10× 10 | 1000 |
| 11 | 11× 11× 11 | 1331 |
| 12 | 12× 12× 12 | 1728 |
| 13 | 13× 13× 13 | 2197 |
| 14 | 14× 14× 14 | 2744 |
| 15 | 15× 15× 15 | 3375 |
| 16 | 16× 16× 16 | 4096 |
| 17 | 17× 17× 17 | 4913 |
| 18 | 18× 18× 18 | 5832 |
| 19 | 19× 19× 19 | 6859 |
| 20 | 20× 20× 20 | 8000 |
| 21 | 21× 21× 21 | 9261 |
| 22 | 22× 22× 22 | 10648 |
| 23 | 23× 23× 23 | 12167 |
| 24 | 24× 24× 24 | 13824 |
| 25 | 25× 25× 25 | 15625 |
| 26 | 26× 26× 26 | 17576 |
| 27 | 27× 27× 27 | 19683 |
| 28 | 28× 28× 28 | 21952 |
| 29 | 29× 29× 29 | 24389 |
| 30 | 30× 30× 30 | 27000 |
| 31 | 31× 31× 31 | 29791 |
| 32 | 32× 32× 32 | 32768 |
| 33 | 33× 33× 33 | 35937 |
| 34 | 34× 34× 34 | 39304 |
| 35 | 35× 35× 35 | 42875 |
| 36 | 36× 36× 36 | 46656 |
| 37 | 37× 37× 37 | 50653 |
| 38 | 38× 38× 38 | 54872 |
| 39 | 39× 39× 39 | 59319 |
| 40 | 40× 40× 40 | 64000 |
| 41 | 41× 41× 41 | 68921 |
| 42 | 42× 42× 42 | 74088 |
| 43 | 43× 43× 43 | 79507 |
| 44 | 44× 44× 44 | 85184 |
| 45 | 45× 45× 45 | 91125 |
| 46 | 46× 46× 46 | 97336 |
| 47 | 47× 47× 47 | 103823 |
| 48 | 48× 48× 48 | 110592 |
| 49 | 49× 49× 49 | 117649 |
| 50 | 50× 50× 50 | 125000 |
How to Find a Perfect Cube?
Every number can be expressed as the product of the power of its Prime factors. If the power of all the Prime factors is in the multiple of 3, then the number is said to be a perfect cube.
1) 15 = 3 × 5
153 = 15 × 15 × 15 = 3 × 5 × 3 × 5 × 3 × 5 = 33 × 53
2) 18 = 2 × 3 × 3
183 = 18 × 18 × 18 = 2 × 3 × 3 × 2 × 3 × 3 × 2 × 3 × 3 = 23 × 33 × 33
From the above examples, we can observe that each prime factor of a number appears three times in the prime factorization of its cube.
Related Articles
- Cube
- Cubes From 1 to 50
- Cube Root 1 to 30
- Squares upto 50
- How to Find Cube Root
- Cube Roots of Unity
- Perfect Numbers
Solved Examples on Perfect Cubes
Question 1: Is the number 600 a perfect cube?
Let us write down, stating the prime factors of the number 600.
\(600 = 2 \times 2\times 2 \times 3 \times 5 \times 5 = 2^{3}.3.5^{2} \)
The number 600 is not a perfect cube as all the prime factors is not a multiple of three.
Question 2: What should be multiplied to the number 120 to make it a perfect cube?
Factors of \( 120 = 2 \times 2 \times 2 \times 3 \times 5 = 2^{3}. 3.5\)
The factor 2 occurs thrice, 3 and 5 occurs only once. So in order to make it a perfect cube we have to multiply 120 with a square of 3 and 5.
Therefore, 120 × 3 × 3 × 5 × 5 =27000
The number 27000 is the required perfect cube.
Application of Perfect Cubes
A cube is a three-dimensional figure which has all the edges of equal length. The volume of a cube is given by the product of its dimensions. For example, for a cube of edge length ‘a’ units, the volume of the cube is given by “a × a × a”which is equal to a3 cubic unit. Similarly, we can calculate the perfect cube of various numbers.
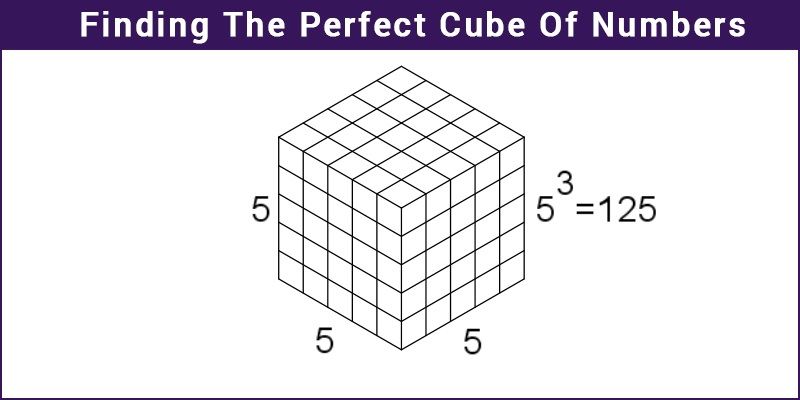
Illustration: Determine the volume of a cube with an edge length of 7 cm.
Solution: The side of the cube is 7 cm.
Volume = side × side × side = 7 × 7 × 7 = 343 cm3.
The numbers such as 1, 8, 27, 64, etc. are known as perfect cubes or cube numbers.
When a cube is broken or cut, total volume still remains the same. Hence, we can observe that to construct a cube of edge length ‘2a’ with cubes of edge length ‘a’ we need to have 8 cubes of edge length a.
This article explains perfect cubes and the method of their calculation. To learn more about other topics download BYJU’S – The Learning App and watch interactive videos. Also, take free tests to practice for exams.
Frequently Asked Questions on Perfect Cubes
What is a perfect cube?
What is the perfect cube of 100?
What are first ten perfect cube numbers?
Which are the perfect cubes among these: 27, 9, 400?
9 and 400 are the perfect squares. 3 x 3 = 9 and 20 x 20 = 400