Graph Theory, in discrete mathematics, is the study of the graph. A graph is determined as a mathematical structure that represents a particular function by connecting a set of points. It is used to create a  pairwise relationship between objects.

The graph is made up of vertices (nodes) that are connected by the edges (lines). The applications of the linear graph are used not only in Maths but also in other fields such as Computer Science, Physics and Chemistry, Linguistics, Biology, etc. In real-life also the best example of graph structure is GPS, where you can track the path or know the direction of the road.

Table of Contents:

• History
• Definition
• Types
• Properties
• Trees Degree Cycle
• Algorithms

What is Graph

In Mathematics, a graph is a pictorial representation of any data in an organised manner. The graph shows the relationship between variable quantities. In a graph theory, the graph represents the set of objects, that are related in some sense to each other. The objects are basically mathematical concepts, expressed by vertices or nodes and the relation between the pair of nodes, are expressed by edges.

History

The history of graph theory states it was introduced by the famous Swiss mathematician named Leonhard Euler, to solve many mathematical problems by constructing graphs based on given data or a set of points. The graphical representation shows different types of data in the form of bar graphs, frequency tables, line graphs, circle graphs, line plots, etc.

Definition

Graph Theory is the study of points and lines. In Mathematics, it is a sub-field that deals with the study of graphs. It is a pictorial representation that represents the Mathematical truth. Graph theory is the study of relationship between the vertices (nodes) and edges (lines).

Formally, a graph is denoted as a pair G(V, E).

Where V represents the finite set vertices and E represents the finite set edges.

Therefore, we can say a graph includes non-empty set of vertices V and set of edges E.

Example

Suppose, a Graph G=(V,E), where

Vertices, V={a,b,c,d} 

Edges, E={{a,b},{a,c},{b,c},{c,d}}

Also, read:

Types of Graph

The graphs are basically of two types, directed and undirected. It is best understood by the figure given below. The arrow in the figure indicates the direction.

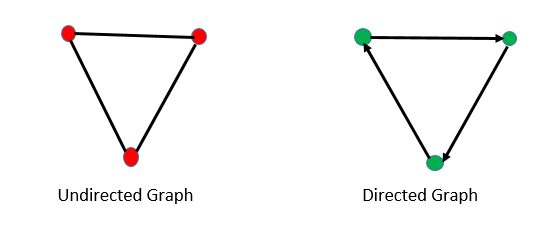
Directed Graph

In graph theory, a directed graph is a graph made up of a set of vertices connected by edges, in which the edges have a direction associated with them.

Undirected Graph

The undirected graph is defined as a graph where the set of nodes are connected together, in which all the edges are bidirectional. Sometimes, this type of graph is known as the undirected network.

Other types of graphs

• Null Graph: A graph that does not have edges.
• Simple graph: A graph that is undirected and does not have any loops or multiple edges.
• Multigraph: A graph with multiple edges between the same set of vertices. It has loops formed. 
• Connected graph: A graph where any two vertices are connected by a path.
• Disconnected graph: A graph where any two vertices or nodes are disconnected by a path.
• Cycle Graph: A graph that completes a cycle. 
• Complete Graph: When each pair of vertices are connected by an edge then such graph is called a complete graph
• Planar graph: When no two edges of a graph intersect and are all the vertices and edges are drawn in a single plane, then such a graph is called a planar graph

Properties of Graph

• The starting point of the network is known as root.
• When the same types of nodes are connected to one another, then the graph is known as an assortative graph, else it is called a disassortative graph.
• A cycle graph is said to be a graph that has a single cycle.
• When all the pairs of nodes are connected by a single edge it forms a complete graph.
• A graph is said to be in symmetry when each pair of vertices or nodes are connected in the same direction or in the reverse direction.
• When a graph has a single graph, it is a path graph.

Trees, Degree and Cycle of Graph

There are certain terms that are used in graph representation such as Degree, Trees, Cycle, etc. Let us learn them in brief.

Trees: A tree in a graph is the connection between undirected networks which are having only one path between any two vertices. It was introduced by British mathematician Arthur Cayley in 1857. The graph trees have only straight lines between the nodes in any specific direction but do not have any cycles or loops. Therefore trees are the directed graph.

Degree: A degree in a graph is mentioned to be the number of edges connected to a vertex. It is denoted deg(v), where v is a vertex of the graph. So basically it the measure of the vertex.

Cycle: A cycle is a closed path in a graph that forms a loop. When the starting and ending point is the same in a graph that contains a set of vertices, then the cycle of the graph is formed. When there is no repetition of the vertex in a closed circuit, then the cycle is a simple cycle. The cycle graph is denoted by C_n.

• A cycle that has an even number of edges or vertices is called Even Cycle.
• A cycle that has an odd number of edges or vertices is called Odd Cycle.

Graph Theory Algorithm

The procedure to draw a graph for any given function or to calculate any function is the algorithm of the graph. Basically, there are predefined steps or sets of instructions that have to be followed to solve a problem using graphical methods. There are different types of algorithms which the graph theory follows, such as;

• Bellman-Ford algorithm
• Borůvka’s algorithm
• Ford–Fulkerson algorithm
• Edmonds–Karp algorithm and many more.

Download BYJU’S The learning App and learn to represent the mathematical equations in a graph.