How to Find Median
Median is one of the measures of central tendency in statistics which gives the value of the middle-most observation in the data. We can calculate the median for different types of data such as ungrouped data and grouped data using relevant formulas. In this article, you will learn how to find the median of given data set along with the solved examples in detail.
Let us recall what is grouped and ungrouped data here.
Grouped data is the data that is categorized into groups after its collection. The raw data can be categorized into various groups using a frequency table.
Ungrouped data, which is also called raw data, is the data that has not been placed in any group or category after its collection. Data is in the form of numbers or characteristics; therefore, the data that has not been put in any type is ungrouped.
Learn: Statistics
Median
The median is the middle number of a group of numbers that have been arranged in order by size. If the number of terms is even, the median is the mean of the two middle numbers.
Steps to find the median of a set of numbers
- Arrange the numbers in order by size.
- If the number of terms is odd, the median is the middle term.
- If the number of terms is even, add the two middlemost terms and then divide by 2.
Learn more about the median of data here.
How to Find Median of Ungrouped Data
For ungrouped data, we can find the median of numbers by considering the number of observations. Let’s learn what is the formula of the median for a set of data values.
When the number of observations is Odd:
First, arrange the data values in ascending order or descending order. Now, count the number of observations in the given set.
Number of observations = n (odd number)
Median = [(n + 1)/2]th observation
Go through the example given below to understand the method of finding the median in this case.
Example 1: The Clintons drove through 7 states in their winter holidays, and the petrol prices were different from state to state. Find the median of these petrol prices.
$1.59, $1.31, $1.96, $3.09, $1.64, $1.55, $2.61
Solution:
Order the given data from smallest to greatest is given by:
$1.31, $1.55, $1.59, $1.64, $1.96, $2.61, $3.09
Here, the number of values = 7 (odd)
Median = [(n + 1)/2]th observation
=[(7 + 1)/2]th observation
= 4th observation
= $1.64
Therefore, the median petrol price is $1.64.
When the number of observations is Even:
After arranging the observations in ascending order or descending order, count the number of observations, i.e. n. If n is an even number, then:
Median = Mean of (n/2)th and [(n/2) + 1]th observation
Let’s have a look at the solved example given below:
Example 2: The points scored by a Kabaddi team in a series of matches are as follows:
17, 2, 7, 27, 15, 5, 14, 8, 10, 24, 48, 10, 8, 7, 18, 28
Find the median of the points scored by the team.
Solution:
Arranging the points scored by the team in ascending order, we get;
2, 5, 7, 7, 8, 8, 10, 10, 14, 15, 17, 18, 24, 27, 28, 4
Number of observations = n = 16
n/2 = 16/2 = 8
(n/2) + 1 = (16/2) + 1 = 8 + 1 = 9
Here, the median will be the average of 8th and 9th observations.
Median = (10 + 14)/2 = 24/2 = 12
Hence, the median of the points scored by the Kabaddi team is 12.
Now, before getting the method of finding the median of grouped data, let’s recall what is cumulative frequency.
Cumulative frequency helps to find the number of observations that lie above (or below) a particular value in a data set. The cumulative frequency is found using a frequency distribution table. The sum obtained by adding each frequency from a frequency distribution table to the sum of its predecessors is called cumulative frequency. The last value will always be equal to the total number of observations since all frequencies are already added to the previous total.
How to Find Median Class of Grouped Data
Suppose N is the total number of frequencies such find the value of N/2.
The class whose cumulative frequency is greater than and near to N/2 is called the median class of grouped data.
How to Find Median of Grouped data
The formula to find the median of given frequency distribution, i.e., for grouped data is:
Median = l + [(N/2 – cf)/f] × h
Here,
l = Lower limit of the median class
N = Sum of frequencies
cf = Cumulative frequency of the class preceding the median class
f = Frequency of median class
h = Class height
Now, go through the below-solved problem to know how to apply the formula to find the median from a frequency table.
Question: Calculate the median for the following distribution.
| Class interval | Frequency |
| 40 – 44 | 1 |
| 45 – 49 | 5 |
| 50 – 54 | 9 |
| 55 – 59 | 12 |
| 60 – 64 | 7 |
| 65 – 69 | 2 |
Solution:
The given frequency distribution has discontinuous classes so let us convert them as continuous classes and calculate the cumulative frequency.
| Class intervals | Frequency | Cumulative frequency |
| 39.5 – 44.5 | 1 | 1 |
| 44.5 – 49.5 | 5 | 6 |
| 49.5 – 54.5 | 9 | 15 |
| 54.5 – 59.5 | 12 | 27 |
| 59.5 – 64.5 | 7 | 34 |
| 64.5 – 69.5 | 2 | 36 |
N = 36
N/2 = 36/2 = 18
Cumulative frequency greater than and nearer to 18 is 27 which belongs to the class interval 54.5 – 59.5.
Thus, median class = 54.5 – 59.5
l = Lower limit of the median class = 54.5
N = Sum of frequencies = 36
cf = Cumulative frequency of the class preceding the median class = 15
f = Frequency of median class = 12
h = Class height = 5
Median = l + [(N/2 – cf)/f] × h
= 54.5 + [(18 – 15)/12] × 5
= 54.5 + [(3 × 5)/12]
= 54.4 + (5/4)
= 54.5 + 1.25
= 55.75
Therefore, the median of the given distribution is 55.75.
To Find The Median For Discrete Data
A set of data is termed discrete if the observations belonging to the set are distinct, separate and unconnected observations. When the data follows a discrete set of observations grouped by size, use the formula ((n+1)/2)th observation for finding the median. Form a cumulative frequency distribution, and the median is that value that corresponds to the cumulative frequency in which ((n+1)/2)th observation lies.
Example:
The given frequency distribution is classified according to the number of cabs provided for different branches of the office. Calculate the median number of cabs.
| No of cabs | No of Branches (f) |
| 3 | 2 |
| 4 | 11 |
| 5 | 15 |
| 6 | 20 |
| 7 | 25 |
| 8 | 18 |
| 9 | 10 |
| Total | 101 |
Solution:
| No of cabs | No of Branches (f) | Cumulative Frequency |
| 3 | 2 | 2 |
| 4 | 11 | 13 |
| 5 | 15 | 28 |
| 6 | 20 | 48 |
| 7 | 25 | 73 |
| 8 | 18 | 91 |
| 9 | 10 | 101 |
| Total | 101 |
Median = ((n+1)/2)th observation
= (101+1)/2
= 102/2
51st observation
Median = 7 because 51st value corresponds to 7.
Watch The Below Video To Learn How To Find The Median In Statistics

Till now, we found the median of data using different approaches and formulas. Let’s have a look at the graphical approach to find the median.
How to Find Median Graphically
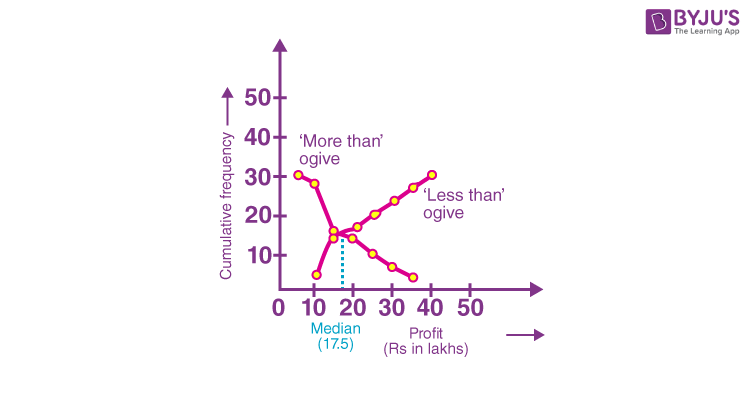
We can find the median of the given distribution graphically by drawing less than and more than Ogive curves. This can be better understood with the help of the below example.
Question: The annual profits earned by 30 shops of a shopping complex in a locality give rise to the following distribution:
| Profit (Rs in Lakhs) | Number of shops (frequency) |
| More than or equal to 5 | 30 |
| More than or equal to 10 | 28 |
| More than or equal to 15 | 16 |
| More than or equal to 20 | 14 |
| More than or equal to 25 | 10 |
| More than or equal to 30 | 7 |
| More than or equal to 35 | 3 |
Draw the less than and more than ogive and hence, obtain the median.
Solution:
The given data can be tabulated as:
| For more than Ogive | For less than Ogive | |||
| Profit (Rs in Lakhs) | Cumulative frequency | Class Interval | Frequency | Cumulative frequency |
| More than or equal to 5 | 30 | 5 – 10 | 2 | 2 |
| More than or equal to 10 | 28 | 10 – 15 | 12 | 14 |
| More than or equal to 15 | 16 | 15 – 20 | 2 | 16 |
| More than or equal to 20 | 14 | 20 – 25 | 4 | 20 |
| More than or equal to 25 | 10 | 25 – 30 | 3 | 23 |
| More than or equal to 30 | 7 | 30 – 35 | 4 | 27 |
| More than or equal to 35 | 3 | 35 – 40 | 3 | 30 |
We first draw the coordinate axes, with lower limits of the profit along the horizontal axis and the cumulative frequency along the vertical axes.
Then, we plot the points (5, 30), (10, 28), (15, 16), (20, 14), (25, 10), (30, 7) and (35, 3) for more than type Ogive.
To draw the less than type Ogive, take the upper limits of class intervals and the corresponding cumulative frequency, such as (10, 2), (15, 14), (20, 16), (25, 20), (30, 23), (35, 27), (40, 30) on the same axes.
No, by plotting all these points, we get the abscissa of their point of intersection is nearly 17.5, which is the median as shown in the below figure.
To learn more statistics concepts, download BYJU’S – The Learning App today!