Indefinite Integrals
In Calculus, the two important processes are differentiation and integration. We know that differentiation is finding the derivative of a function, whereas integration is the inverse process of differentiation. Here, we are going to discuss the important component of integration called “integrals” here.
Suppose a function f is differentiable in an interval I, i.e., its derivative f’ exists at each point of I. In that case, a simple question arises: Can we determine the function for obtained f’ at each point? The functions that could have provided function as a derivative are called antiderivatives (or primitive). The formula that gives all these antiderivatives is called the indefinite integral of the function. And such a process of finding antiderivatives is called integration.
The integrals are generally classified into two types, namely:
- Definite Integral
- Indefinite Integral
Here, let us discuss one of the integral types called “Indefinite Integral” with definition and properties in detail.
Indefinite Integrals Definition
An integral which is not having any upper and lower limit is known as an indefinite integral.
Mathematically, if F(x) is any anti-derivative of f(x) then the most general antiderivative of f(x) is called an indefinite integral and denoted,
∫f(x) dx = F(x) + C
We mention below the following symbols/terms/phrases with their meanings in the table for better understanding.
| Symbols/Terms/Phrases | Meaning |
| ∫ f(x) dx | Integral of f with respect to x |
| f(x) in ∫ f(x) dx | Integrand |
| x in ∫ f(x) dx | Variable of integration |
| An integral of f | A function F such that F′(x) = f (x) |
| Integration | The process of finding the integral |
| Constant of Integration | Any real number C, considered as constant function |
Anti derivatives or integrals of the functions are not unique. There exist infinitely many antiderivatives of each of certain functions, which can be obtained by choosing C arbitrarily from the set of real numbers. For this reason, C is customarily referred to as an arbitrary constant. C is the parameter by which one gets different antiderivatives (or integrals) of the given function.
Get Indefinite Integral calculator here.
Indefinite Properties
Let us now look into some properties of indefinite integrals.
Property 1: The process of differentiation and integration are inverses of each other in the sense of the following results:

And
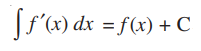
where C is any arbitrary constant.
Let us now prove this statement.
Proof: Consider a function f such that its anti-derivative is given by F, i.e.
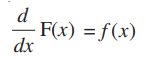
Then,
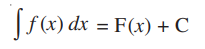
On differentiating both the sides with respect to x we have,
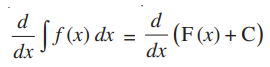
As we know, the derivative of any constant function is zero. Thus,
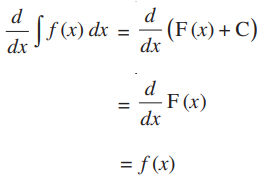
The derivative of a function f in x is given as f’(x), so we get;
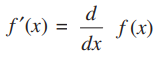
Therefore,
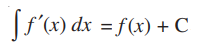
Hence, proved.
Property 2: Two indefinite integrals with the same derivative lead to the same family of curves, and so they are equivalent.
Proof: Let f and g be two functions such that
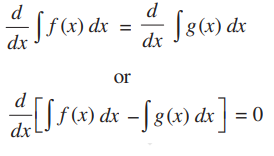
Now,
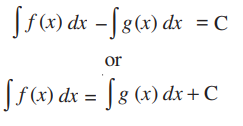
where C is any real number.
From this equation, we can say that the family of the curves of [ ∫ f(x)dx + C3, C3 ∈ R] and [ ∫ g(x)dx + C2, C2 ∈ R] are the same.
Therefore, we cay say that, ∫ f(x)dx = ∫ g(x)dx
Property 3: The integral of the sum of two functions is equal to the sum of integrals of the given functions, i.e.,
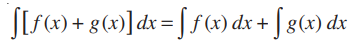
Proof:
From the property 1 of integrals we have,
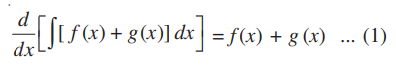
Also, we can write;
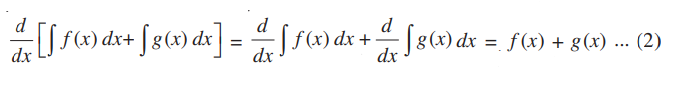
From (1) and (2),
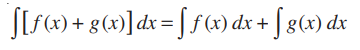
Hence proved.
Property 4: For any real value of p,
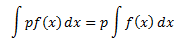
Proof: From property 1 we can say that
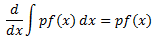
Also,
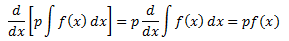
From property 2 we can say that
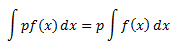
Property 5:
For a finite number of functions f1, f2…. fn and the real numbers p1, p2…pn,
∫[p1f1(x) + p2f2(x)….+pnfn(x) ]dx = p1∫f1(x)dx + p2∫f2(x)dx + ….. + pn∫fn(x)dx
Indefinite Integral Formulas
The list of indefinite integral formulas are
- ∫ 1 dx = x + C
- ∫ a dx = ax + C
- ∫ xn dx = ((xn+1)/(n+1)) + C ; n ≠ 1
- ∫ sin x dx = – cos x + C
- ∫ cos x dx = sin x + C
- ∫ sec2x dx = tan x + C
- ∫ cosec2x dx = -cot x + C
- ∫ sec x tan x dx = sec x + C
- ∫ cosec x cot x dx = -cosec x + C
- ∫ (1/x) dx = ln |x| + C
- ∫ ex dx = ex + C
- ∫ ax dx = (ax/ln a) + C ; a > 0, a ≠ 1
Indefinite Integrals Examples
Go through the following indefinite integral examples and solutions given below:
Example 1:
Evaluate the given indefinite integral problem: ∫6x5 -18x2 +7 dx
Solution:
Given,
∫6x5 -18x2 +7 dx
Integrate the given function, it becomes:
∫6x5 -18x2 +7 dx = 6(x6/6) – 18 (x3/3) + 7x + C
Note: Don’t forget to put the integration constant “C”
After simplification, we get the solution
Thus, ∫6x5 -18x2 +7 dx = x6-6x3+ 7x+ C
Example 2:
Evaluate f(x), given that f ‘(x) = 6x8 -20x4 + x2 + 9
Solution:
Given,
f ‘(x) = 6x8 -20x4 + x2 + 9
We know that, the inverse process of differentiation is an integration.
Thus, f(x) = ∫f ‘(x) dx=∫[6x8 -20x4 + x2 + 9] dx
f(x) = (2/3)x9 – 4x5 +(1/3)x3 + 9x+ C
Indefinite Integral vs Definite Integral
An indefinite integral is a function that practices the antiderivative of another function. It can be visually represented as an integral symbol, a function, and then a dx at the end. The indefinite integral is an easier way to signify getting the antiderivative. The indefinite integral is similar to the definite integral, yet the two are not the same. The below figure shows the difference between definite and indefinite integral.
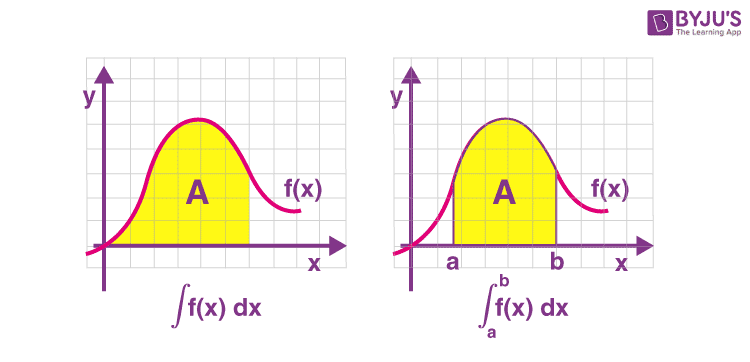
Video Lesson
Indefinite Integration

Learn how to evaluate Definite Integrals here. To learn more about indefinite integrals, download BYJU’S- The Learning App.
Frequently Asked Questions – FAQs
How do you find the indefinite integral?
∫f(x)dx = F(x) + C, where C is any real number.
We generally use suitable formulas which help in getting the antiderivative of the given function.
The result of the indefinite integral is a function.