Octal Number System
Octal Number System has a base of eight and uses the number from 0 to 7. The octal numbers, in the number system, are usually represented by binary numbers when they are grouped in pairs of three. For example, 128 is expressed as 0010102, where 1 is equivalent to 001 and 2 is equivalent to 010.
| Octal Number System |
| Base – 8 |
| Octal Symbol – 0, 1, 2, 3, 4, 5, 6 and 7 |
| Table of Contents: |
Apart from octal number system, there are other number systems in Maths, such as:
Definition
A number system which has its base as ‘eight’ is called an Octal number system. It uses numbers from 0 to 7. Let us take an example, to understand the concept. As we said, any number with base 8 is an octal number like 248, 1098, 558, etc.
Like Octal number is represented with base 8, in the same way, a binary number is represented with base 2, decimal number with base 10 and the hexadecimal number is represented with base 16. Examples for these number systems are:
- 222 is a binary number
- 10010 is a decimal number
- 4016 is a hexadecimal number
If we solve an octal number, each place is a power of eight.
- 1248= 1 × 82 + 2 × 81 + 4 × 80
Octal Numbers System Table
We use only 3 bits to represent Octal Numbers. Each group will have a distinct value between 000 and 111.
|
Octal Digital Value |
Binary Equivalent |
| 0 | 000 |
| 1 | 001 |
| 2 | 010 |
| 3 | 011 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
Note: Octal number system supports only digits from 0 to 7. Beyond 7, such as 8 and 9 are not octal digits. For example, 19 is not an octal number by 10 is an octal number.
Decimal to Octal Number
To convert decimal to octal number, octal dabble method is used. In this method, the decimal number is divided by 8 each time, it yields or gives a remainder. The first remainder we get is the least significant digit(LSD) and the last remainder is the most significant digit(MSD). Let us understand the conversion with the help example.
Solved Example
Problem: Suppose 560 is a decimal number. Convert it into an octal number.
Solution: If 560 is a decimal number, then,
560/8=70 and remainder is 0
70/8=8 and remainder is 6
8/8=1 and remainder is 0
And 1/8=0 and remainder is 1
So the octal number starts from MSD to LSD, i.e. 1060
Therefore, 56010 = 10608
Problem: Convert 0.52 into an octal number.
Solution: The fraction part of the decimal number has to be multiplied by 8.
0.52 × 8=0.16 with carry 4
0.16 × 8=0.28 with carry 1
0.28 × 8=0.24 with carry 2
0.24 × 8=0.92 with carry 1
So, for the fractional octal number, we read the generated carry from up to down.
Therefore, 4121 is the octal number.
Octal to Decimal
To convert an octal number to decimal number we need to multiply each digit of the given octal with the reducing power of 8.
Let us learn here, conversion of Octal number to Decimal Number or base 8 to base 10.
Solved Examples
Example 1: Suppose 2158 is an octal number, then it’s decimal form will be,
2158 = 2 × 82 + 1 × 81 + 5 × 80
= 2 × 64+ 1 × 8 + 5 × 1 = 128 + 8 + 5
= 14110
Example 2: Let 125 is an octal number denoted by 1258. Find the decimal number.
1258 = 1× 82 + 2 × 81 + 5 × 80
= 1 × 64 + 2 × 8 + 5 × 1 = 64+16+5
=8510
Binary To Octal Number
A binary number can be converted into an octal number, with the help of the below-given table.
|
Octal Number |
Equivalent Binary Number |
|
0 |
0 |
|
1 |
1 |
|
2 |
10 |
|
3 |
11 |
| 4 |
100 |
| 5 |
101 |
| 6 |
110 |
| 7 |
111 |
Solved Example
Example: Convert (100010)2 to octal number.
Solution: With the help of the table we can write,
100→4
and 010→2
Therefore,(100010)2 = 42
Similarly, we can convert an octal number to binary number with the help of the table.
Octal to Hexadecimal Number
Hexadecimal numbers consist of numbers and alphabets. It is represented with base 16. The numbers from 0-9 are represented in the usual form, but from 10 to 15, it is denoted as A, B, C, D, E, F. Conversion of the octal number to hexadecimal requires two steps.
- First, convert octal number to decimal number.
- Then, convert decimal number to hexadecimal number.
Let us understood with the help of an example. We will take the same example, where we have converted octal number to decimal, such as;
(55)8 = (45)10
Now, convert (45)10 into a hexadecimal number by dividing 45 by 16 until you get remainder less than 16.
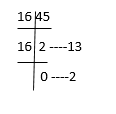
Therefore, we can write, (45)10 = (2D)16
Octal Multiplication Table
| * | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 0 | 2 | 4 | 6 | 10 | 12 | 14 | 16 |
| 3 | 0 | 3 | 6 | 11 | 14 | 17 | 22 | 25 |
| 4 | 0 | 4 | 10 | 14 | 20 | 24 | 30 | 34 |
| 5 | 0 | 5 | 12 | 17 | 24 | 31 | 36 | 43 |
| 6 | 0 | 6 | 14 | 22 | 30 | 36 | 44 | 52 |
| 7 | 0 | 7 | 16 | 25 | 34 | 43 | 52 | 61 |
Applications
The octal Number system is widely used in computer application sectors and also in the aviation sector to use the number in the form of code.
Based on octal number system applications, several computing systems are developed. All the modern generation computing system uses 16-bit, 32-bit or 64-bit word which is further divided into 8-bit words. Similarly, for various programming languages, octal numbers are used to do coding or to write the encrypted language, which is only understood by the computing machine.
Also in the aviation sector or field or say aviation industry, Transponders used in the aircraft transmits a code which is expressed as four octal digit number. These codes are interrogated by ground radar.
Importance
Octal number system uses less digits (3-bits) than hexadecimal numbers (4-bits), which is one of the advantages. It is therefore, there will be less computations and possibility of occurrence of error will degrade.
Because of less digits, it is also easy to convert octal to any other number system and vice-versa.
One of the disadvantages is that computers do not understand the octal numbers in a direct way and hence it has to be converted into binary numbers first.
Problems and Solutions
Q.1: Convert 2758 to decimal number.
Solution: 2 x 82 + 7 x 81 + 5 x 80
= 64×2 + 8×7 + 1×5
= 128 + 56 + 5
= 189
Therefore, 2758 = 18910
Q.2: Convert decimal number 139 into equivalent octal number.
Solution: We need to divide 139 by 8 repeatedly, till the quotient is 0.
| 8 | 139 | Remainder |
| 8 | 17 | 3 |
| 8 | 2 | 1 |
| 0 | 2 |
Now take the remainders from down to up to get the equivalent octal number.
13910 = 2138
Q.3: Convert the octal number 540 into binary number.
Solution: Given, 540 is the octal number
By the octal number table, we can get the binary equivalent of each digit.
5 → 101
4 → 100
0 → 000
Therefore,
5408 = 1011000002
Practice Questions
Convert the following octal numbers into its equivalent decimal number.
- 238 (Answer: 1910)
- 7708 (Answer: 50410)
- 1528 (Answer: 10610)
Convert the following octal numbers into hexadecimal numbers.
- 238 (Answer: 1316)
- 7708 (Answer: 1F816)
- 1528 (Answer: 6A16)
Also, study-related topics on number systems by downloading BYJU’S -The Learning App.
Frequently Asked Questions – FAQs
What is an octal number system?
What is the use of octal numbers?
What is the importance of octal number system?
What is the octal form of decimal number 19?
19/8 = 2, Remainder = 3
2/8 = 0, Remainder = 2
Therefore, 1910 = 238
What are 4 types of number system?
Octal Number system
Decimal number system
Hexadecimal number system
What is 138 in binary?
1 → 001
3 → 011
Therefore, clubbing both the numbers we get:
138 = 0010112
Or 138 = 10112
What is the binary number 1111 equivalent to in octal number system?
001111 → 001 111 → 17
(1111)2 → (17)2