The properties of multiplication of integers refer to the product of two or more integers. To recall, the set of numbers that consist of natural numbers, the additive inverse of natural numbers and zero are known as integers. Thus, integers can either be positive or negative, which is represented on a number line. They are usually represented by Z. The examples of integers are 1, 2, 3, 0, -10, -7, etc.

The four basic mathematical operations i.e. Addition, subtraction, multiplication, division and the properties related to these operations can be applied to integers as well.

The rules of the multiplication of integers are explained here in this article. To multiply any two integers, we should learn the basic properties of multiplication such as commutative property, associative property, etc. Learning these properties will help the students of Class 1 to 10, to solve multiplication problems easily.

Multiplication of Integers

Multiplication is basically the repeated addition of numbers. For example, if we say, 2 multiplied by 3, it means 2 is added to itself three times.
2 x 3 = 2 + 2 + 2 = 6

Therefore multiplication of integers is the repeated addition as:

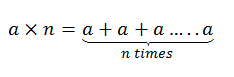
Where a and n are both integers.

What are the Properties of Multiplication of Integers?

The properties of multiplication of integers are:

• Closure property
• Commutative property
• Associative property
• Distributive property
• Multiplication by zero
• Multiplicative identity

Some of the properties of addition such as commutative and associative properties are also similar to those properties of multiplication. Thus, becomes easier to remember such properties.

Closure Property of Multiplication

According to this property, if two integers a and b are multiplied then their resultant a × b is also an integer. Therefore, integers are closed under multiplication.

a × b is an integer, for every integer a and b

Examples:

• 2 x -1 = -2
• 4 x 5 = 20

Commutative Property of Multiplication

The commutative property of multiplication of integers states that altering the order of operands or the integers does not affect the result of the multiplication.

a × b = b × a, for every integer a and b

Examples:

• 3 x 4 = 4 x 3 (=12)
• 5 x 2 = 2 x 5 (=10)

Associative Property of Multiplication

The result of the product of three or more integers is irrespective of the grouping of these integers. In general, if a, b and c are three integers then,

a × (b × c) = (a × b) × c

Examples:

• 3 x (4 x 5) = (3 x 4) x 5 (=60)
• -2 x (-1 x -3) = (-2 x -1) x -3 (= -6)

Distributive Property of Multiplication

According to the distributive property of multiplication of integers, if a, b and c are three integers then,

a× (b + c) = (a × b) + (a × c)

Example:

• 2 x (2 + 3) = (2 x 2) + (2 x 3)
• 2 x 6 = 4 + 6
• 12 = 12

Multiplication by zero

On multiplying any integer by zero the result is always zero. In general, if a and b are two integers then,

a × 0 = 0 × a = 0

Examples:

• 4 x 0 = 0
• -10 x 0 = 0
• 100 x 0 = 0

Thus, we can see, any integer whether it is the smallest one or the largest one, when multiplied by zero, results in zero only.

Multiplicative Identity of Integers

On multiplying any integer by 1 the result obtained is the integer itself. In general, if a and b are two integers then,

a × 1 = 1 × a = a

Therefore 1 is the Multiplicative Identity of Integers.

Examples:

• 23 x 1 = 23
• 44 x 1 = 44
• -79 x 1 = -79
• -105 x 1 = -105

Other Properties of Multiplication

1. If a, b and c are the integers and a > b, then;
a x c > b x c

Example: If 5 > 4

5 x 2 = 10

4 x 2 = 8

Therefore,

5 x 2 > 4 x 2

2. Change of Sign Property.

• Multiplication of two positive integers is always positive
• Multiplication of two negative integers is always negative
• Multiplication of a positive integer and a negative integer results in a negative integer.

Examples:

• (+2) x (+ 4) = +8
• (-2) x (-4) = +8
• (-2) x (+4) = -8

Related Articles

• Integers
• Whole Numbers
• Natural Numbers
• Real Numbers
• Number System
• Arithmetic Operations

Solved Examples on Properties of Multiplication

Find the product using suitable properties.

Q.1. 26 x (-48) + (-48) x (-36).

Solution: Given, 26 x (-48) + (-48) x (-36)

On rearranging the given expression, using commutative property, we get;

⇒ (-48) x (26) + (-48) x (-36)

Again using distributive property, we get;

⇒ (-48) [26 + (-36)]

⇒ (-48) x [26 – 36]

⇒ (-48) x (-10)

⇒ 480

Q.2. (-25) x (101).

Solution: Given, (-25) x 101

We can write the above expression as:

⇒ (-25) x (100+1)

Using distributive property, we get;

⇒ (-25 x 100) + (-25 x 1)

⇒ -2500 + (-25)

⇒ -2500 – 25

⇒ -2525

Q.3. 4 x 23 x (-125).

Solution: Given, 4 x 23 x (-125)

Using associative property, we can arrange the given expression as:

⇒ 23 x 4 x (-125)

⇒ 23 x [4 x (-125)]

⇒ 23 x (-500)

⇒ -11500

Worksheet on Properties of Multiplication

Fill in the blanks:

• 8 x 5 = ___ x 8
• (1 x 2) x 9 = 1 x (2 x __)
• 10 x (10 + 10) = ___
• 100 x 0 = _____
• 121 x 1 = ____
• 9 x 10 = ____
• 3 x -8 = ____

Find the product of the following:

• 2 x 3 = ?
• 4 x 8 = ?
• 10 x 10 x 10 = ?
• 15 x 10 = ?

Which properties of multiplication are these?

• 2190 x 1 = 2190 ___________
• 3 x 100 = 100 x 3 __________
• (10 x 40) x 2 = 10 x (40 x 2) ______________
• 1200 x 0 = 0 ___________

Keep visiting BYJU’S and Subscribe to our YouTube channel for learning number systems and other mathematical topics in a fun and engaging way. Also, register now to get access to 1000+ hours of engaging video content.