Sec 90

Home → Sec 90

The sec of an angle in a right triangle is the ratio of the length of the hypotenuse to the length of the adjacent side. In other words, secant is the reciprocal of the cosine function.

Consider a triangle ABC right-angled at B and θ is an acute angle at B as shown in the figure given below.

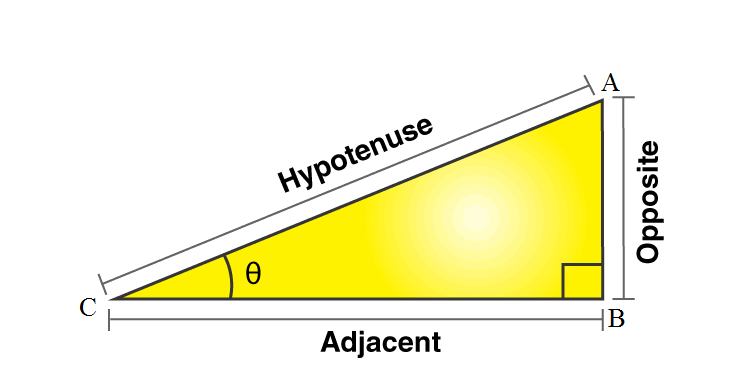
Sec θ = Hypotenuse / Adjacent side

Secant can be easily replaced by cos x in this way, Sec θ = 1 / Cos θ.

Sec 90 Degrees

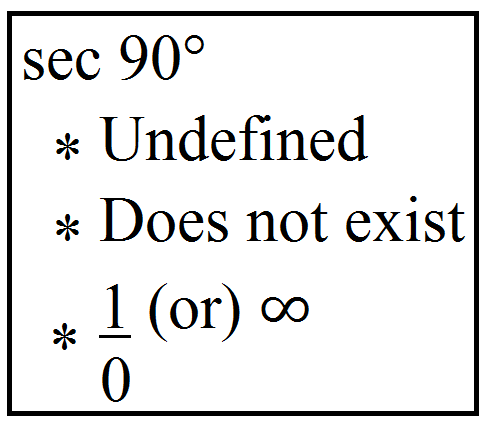
The value of sec 90 degrees is undefined.

Sec 90 Value

The value of Sec 90 (in radians) = -2.2317761286…

The Inverse Sec x Formula –

For every trigonometric function, there is always an inverse function that works in reverse. These all inverse functions have the name as an arc in starting. The inverse name of sec is arcsec.

The value of Secant 90 degree cannot be calculated and is undefined in the trigonometric table.

How to Calculate Sec 90?

As the angle is between 0 and 90 degrees, it is located in the 1st quadrant, where the value of sin, cos and tan are positive.

90 degrees is always the right angle.

Sec x = 1/cos x

Sec 90° = 1/ cos 90°

Sec 90° = 1/ 0

Sec 90° = undefined

Sec 90 minus Theta

Let us derive the formula of sec 90 degrees minus theta here.

Sec 90° – Theta = sec(90° – θ)

= sec(1 × 90° – θ)

Here, 90° is multiplied by 1, an odd number so sec will change to cosec. Also, 90° – θ comes in the first quadrat. That means, all trigonometry ratios are positive.

So, sec(90° – θ) = cosec θ

Therefore, Sec 90 – Theta is equal to Cosec theta.

In the same way, we can derive the formula for sec 90 degrees plus theta.

sec(90° + θ) = -cosec θ

Examples on Sec 90 Value

Question 1:

What is the value of Sec(270 – x) Sec(90 – x) – tan (270 – x) tan (90 – x)?

Solution: Sec(270 – x) Sec(90 – x) – tan (270 – x) tan (90 – x)=?

=( – cosec x cosec x) – ( – cot x cot x)

= -cosec ² x + cot²x

= – 1

Question 2:

Find the value of sin 30° + 1/sec 90°.

Solution:

We know that, sec x = 1/cos x or cos x = 1/sec x

Thus, sin 30° + 1/sec 90° = sin 30° + cos 90°

= 1/2 + 0

= 1/2